Chapter 5 Optimal Individualized Treatment Regimes

Ivana Malenica

Based on the tmle3mopttx R package by Ivana Malenica, Jeremy Coyle, and Mark van der Laan.

Updated: 2020-02-20

5.1 Learning Objectives

By the end of this lesson you will be able to:

  1. Differentiate dynamic and optimal dynamic treatment interventions from static interventions.
  2. Explain the benefits and challenges associated with using optimal individualized treatment regimes in practice.
  3. Contrast the impact of implementing an optimal individualized treatment regime in the population with the impact of implementing static and dynamic treatment regimes in the population.
  4. Estimate causal effects under optimal individualized treatment regimes with the tmle3mopttx R package.
  5. Implement optimal individualized treatment rules based on sub-optimal rules, or “simple” rules, and recognize the practical benefit of these rules.
  6. Construct “realistic” optimal individualized treatment regimes that respect real data and subject-matter knowledge limitations on interventions by only considering interventions that are supported by the data.
  7. Measure variable importance as defined in terms of the optimal individualized treatment interventions.

5.2 Introduction to Optimal Individualized Interventions

Identifying which intervention will be effective for which patient based on lifestyle, genetic and environmental factors is a common goal in precision medicine. One opts to administer the intervention to individuals who will benefit from it, instead of assigning treatment on a population level.

  • This aim motivates a different type of an intervention, as opposed to the static exposures we might be used to.

  • In this chapter, we learn about dynamic (individualized) interventions that tailor the treatment decision based on the collected covariates.

  • In the statistics community, such a treatment strategy is termed individualized treatment regimes (ITR), and the (counterfactual) population mean outcome under an ITR is the value of the ITR.

  • Even more, suppose one wishes to maximize the population mean of an outcome, where for each individual we have access to some set of measured covariates. An ITR with the maximal value is referred to as an optimal ITR or the optimal individualized treatment. Consequently, the value of an optimal ITR is termed the optimal value, or the mean under the optimal individualized treatment.

  • One opts to administer the intervention to individuals who will profit from it, instead of assigning treatment on a population level. But how do we know which intervention works for which patient?

  • For example, one might seek to improve retention in HIV care. In a randomized clinical trial, several interventions show efficacy- including appointment reminders through text messages, small cash incentives for on time clinic visits, and peer health workers.

  • Ideally, we want to improve effectiveness by assigning each patient the intervention they are most likely to benefit from, as well as improve efficiency by not allocating resources to individuals that do not need them, or would

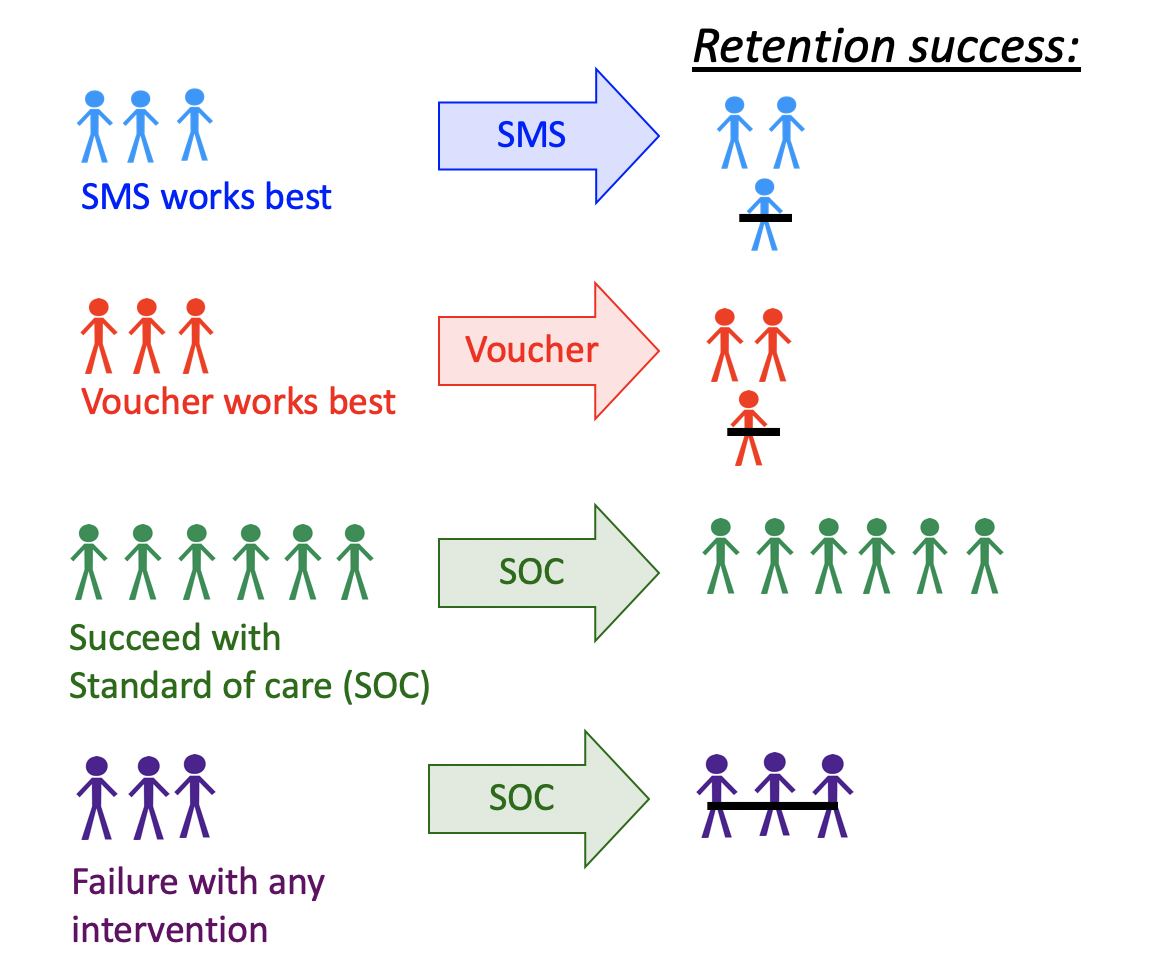
Illustration of a Dynamic Treatment Regime in a Clinical Setting

Figure 5.1: Illustration of a Dynamic Treatment Regime in a Clinical Setting

This aim motivates a different type of intervention, as opposed to the static exposures we might be used to.

  • In this chapter, we examine multiple examples of optimal individualized treatment regimes and estimate the mean outcome under the ITR where the candidate rules are restricted to depend only on user-supplied subset of the baseline covariates.

  • In order to accomplish this, we present the tmle3mopttx R package, which features an implementation of a recently developed algorithm for computing targeted minimum loss-based estimates of a causal effect based on optimal ITR for categorical treatment.

  • In particular, we will use tmle3mopttx to estimate optimal ITR and the corresponding population value, construct realistic optimal ITRs, and perform variable importance in terms of the mean under the optimal individualized treatment.

5.3 Data Structure and Notation

  • Suppose we observe \(n\) independent and identically distributed observations of the form \(O=(W,A,Y) \sim P_0\). \(P_0 \in \mathcal{M}\), where \(\mathcal{M}\) is the fully nonparametric model.

  • Denote \(A \in \mathcal{A}\) as categorical treatment, where \(\mathcal{A} \equiv \{a_1, \ldots, a_{n_A} \}\) and \(n_A = |\mathcal{A}|\), with \(n_A\) denoting the number of categories.

  • Denote \(Y\) as the final outcome, and \(W\) a vector-valued collection of baseline covariates.

  • The likelihood of the data admits a factorization, implied by the time ordering of \(O\). \[\begin{equation*}\label{eqn:likelihood_factorization} p_0(O) = p_{Y,0}(Y|A,W) p_{A,0}(A|W) p_{W,0}(W) = q_{Y,0}(Y|A,W) q_{A,0}(A|W) q_{W,0}(W), \end{equation*}\]

  • Consequently, we define \(P_{Y,0}(Y|A,W)=Q_{Y,0}(Y|A,W)\), \(P_{A,0}(A|W)=g_0(A|W)\) and \(P_{W,0}(W)=Q_{W,0}(W)\) as the corresponding conditional distributions of \(Y\), \(A\) and \(W\).

  • We also define \(\bar{Q}_{Y,0}(A,W) \equiv E_0[Y|A,W]\).

  • Finally, denote \(V\) as \(V \in W\), defining a subset of the baseline covariates the optimal individualized rule depends on.

5.4 Defining the Causal Effect of an Optimal Individualized Intervention

  • Consider dynamic treatment rules \(V \rightarrow d(V) \in \{a_1, \ldots, a_{n_A} \} \times \{1\}\), for assigning treatment \(A\) based on \(V \in W\).

  • Dynamic treatment regime may be viewed as an intervention in which \(A\) is set equal to a value based on a hypothetical regime \(d(V)\), and \(Y_{d(V)}\) is the corresponding counterfactual outcome under \(d(V)\).

  • The goal of any causal analysis motivated by an optimal individualized intervention is to estimate a parameter defined as the counterfactual mean of the outcome with respect to the modified intervention distribution.

  • Recall causal assumptions:

  1. Consistency: \(Y^{d(v_i)}_i = Y_i\) in the event \(A_i = d(v_i)\), for \(i = 1, \ldots, n\).
  2. Stable unit value treatment assumption (SUTVA): \(Y^{d(v_i)}_i\) does not depend on \(d(v_j)\) for \(i = 1, \ldots, n\) and \(j \neq i\), or lack of interference.
  3. Strong ignorability: \(A \perp \!\!\! \perp Y^{d(v)} \mid W\), for all \(a \in \mathcal{A}\).
  4. Positivity (or overlap): \(P_0(\min_{a \in \mathcal{A}} g_0(a|W) > 0)=1\)

  • Here, we also assume non-exceptional law is in effect.

  • We are primarily interested in the value of an individualized rule, \[E_0[Y_{d(V)}] = E_{0,W}[\bar{Q}_{Y,0}(A=d(V),W)].\]

  • The optimal rule is the rule with the maximal value: \[d_{opt}(V) \equiv \text{argmax}_{d(V) \in \mathcal{D}} E_0[Y_{d(V)}] \] where \(\mathcal{D}\) represents the set of possible rules, \(d\), implied by \(V\).

  • The target causal estimand of our analysis is: \[\psi_0 := E_0[Y_{d_{opt}(V)}] = E_{0,W}[\bar{Q}_{Y,0}(A=d_{opt}(V),W)].\]

  • General, high-level idea:

  1. Learn the optimal ITR using the Super Learner.

  2. Estimate its value with the cross-validated Targeted Minimum Loss-based Estimator (CV-TMLE).

5.4.1 Why CV-TMLE?

  • CV-TMLE is necessary as the non-cross-validated TMLE is biased upward for the mean outcome under the rule, and therefore overly optimistic.

  • More generally however, using CV-TMLE allows us more freedom in estimation and therefore greater data adaptivity, without sacrificing inference!

5.5 Binary Treatment

  • How do we estimate the optimal individualized treatment regime? In the case of a binary treatment, a key quantity for optimal ITR is the blip function.

  • Optimal ITR ideally assigns treatment to individuals falling in strata in which the stratum specific average treatment effect, the blip function, is positive and does not assign treatment to individuals for which this quantity is negative.

  • We define the blip function as: \[\bar{Q}_0(V) \equiv E_0[Y_1-Y_0|V] \equiv E_0[\bar{Q}_{Y,0}(1,W) - \bar{Q}_{Y,0}(0,W) | V], \] or the average treatment effect within a stratum of \(V\).

  • Optimal individualized rule can now be derived as \(d_{opt}(V) = I(\bar{Q}_{0}(V) > 0)\).

  • Relying on the Targeted Maximum Likelihood (TML) estimator and the Super Learner estimate of the blip function, we follow the below steps in order to obtain value of the ITR:

  1. Estimate \(\bar{Q}_{Y,0}(A,W)\) and \(g_0(A|W)\) using sl3. We denote such estimates as \(\bar{Q}_{Y,n}(A,W)\) and \(g_n(A|W)\).

  2. Apply the doubly robust Augmented-Inverse Probability Weighted (A-IPW) transform to our outcome, where we define:

\[D_{\bar{Q}_Y,g,a}(O) \equiv \frac{I(A=a)}{g(A|W)} (Y-\bar{Q}_Y(A,W)) + \bar{Q}_Y(A=a,W)\]

Note that under the randomization and positivity assumptions we have that \(E[D_{\bar{Q}_Y,g,a}(O) | V] = E[Y_a |V].\) We emphasize the double robust nature of the A-IPW transform: consistency of \(E[Y_a |V]\) will depend on correct estimation of either \(\bar{Q}_{Y,0}(A,W)\) or \(g_0(A|W)\). As such, in a randomized trial, we are guaranteed a consistent estimate of \(E[Y_a |V]\) even if we get \(\bar{Q}_{Y,0}(A,W)\) wrong!

Using this transform, we can define the following contrast:

\[D_{\bar{Q}_Y,g}(O) = D_{\bar{Q}_Y,g,a=1}(O) - D_{\bar{Q}_Y,g,a=0}(O)\]

We estimate the blip function, \(\bar{Q}_{0,a}(V)\), by regressing \(D_{\bar{Q}_Y,g}(O)\) on \(V\) using the specified sl3 library of learners and an appropriate loss function.

  1. Our estimated rule is \(d(V) = \text{argmax}_{a \in \mathcal{A}} \bar{Q}_{0,a}(V)\).

  2. We obtain inference for the mean outcome under the estimated optimal rule using CV-TMLE.

5.5.1 Evaluating the Causal Effect of an optimal ITR with Binary Treatment

To start, let us load the packages we will use and set a seed for simulation:

5.5.1.1 Simulate Data

Our data generating distribution is of the following form:

\[W \sim \mathcal{N}(\bf{0},I_{3 \times 3})\] \[P(A=1|W) = \frac{1}{1+\exp^{(-0.8*W_1)}}\] \[P(Y=1|A,W) = 0.5\text{logit}^{-1}[-5I(A=1)(W_1-0.5)+5I(A=0)(W_1-0.5)] + 0.5\text{logit}^{-1}(W_2W_3)\]

  • The above composes our observed data structure \(O = (W, A, Y)\).

  • Note that the mean under the true optimal rule is \(\psi=0.578\) for this data generating distribution.

  • Next, we specify the role that each variable in the data set plays as the nodes in a DAG.

  • We now have an observed data structure (data), and a specification of the role that each variable in the data set plays as the nodes in a DAG.

5.5.1.3 Targeted Estimation of the Mean under the Optimal Individualized Interventions Effects

  • To start, we will initialize a specification for the TMLE of our parameter of interest simply by calling tmle3_mopttx_blip_revere.

  • We specify the argument V = c("W1", "W2", "W3") when initializing the tmle3_Spec object in order to communicate that we’re interested in learning a rule dependent on V covariates.

  • We also need to specify the type of blip we will use in this estimation problem, and the list of learners used to estimate relevant parts of the likelihood and the blip function.

  • In addition, we need to specify whether we want to maximize or minimize the mean outcome under the rule (maximize=TRUE).

  • If complex=FALSE, tmle3mopttx will consider all the possible rules under a smaller set of covariates including the static rules, and optimize the mean outcome over all the suboptimal rules dependent on \(V\).

  • If realistic=TRUE, only treatments supported by the data will be considered, therefore alleviating concerns regarding practical positivity issues.

A tmle3_Fit that took 1 step(s)
   type         param  init_est  tmle_est         se     lower   upper
1:  TSM E[Y_{A=NULL}] 0.4316408 0.5585492 0.02704684 0.5055384 0.61156
   psi_transformed lower_transformed upper_transformed
1:       0.5585492         0.5055384           0.61156

We can see that the confidence interval covers our true mean under the true optimal individualized treatment!

5.6 Categorical Treatment

QUESTION: Can we still use the blip function if the treatment is categorical?

  • In this section, we consider how to evaluate the mean outcome under the optimal individualized treatment when \(A\) has more than two categories!

  • We define pseudo-blips as vector valued entities where the output for a given \(V\) is a vector of length equal to the number of treatment categories, \(n_A\). As such, we define it as: \[\bar{Q}_0^{pblip}(V) = \{\bar{Q}_{0,a}^{pblip}(V): a \in \mathcal{A} \}\]

  • We implement three different pseudo-blips in tmle3mopttx.

  1. Blip1 corresponds to choosing a reference category of treatment, and defining the blip for all other categories relative to the specified reference: \[\bar{Q}_{0,a}^{pblip-ref}(V) \equiv E_0(Y_a-Y_0|V)\]

  2. Blip2 approach corresponds to defining the blip relative to the average of all categories: \[\bar{Q}_{0,a}^{pblip-avg}(V) \equiv E_0(Y_a- \frac{1}{n_A} \sum_{a \in \mathcal{A}} Y_a|V)\]

  3. Blip3 reflects an extension of Blip2, where the average is now a weighted average: \[\bar{Q}_{0,a}^{pblip-wavg}(V) \equiv E_0(Y_a- \frac{1}{n_A} \sum_{a \in \mathcal{A}} Y_{a} P(A=a|V) |V)\]

5.6.1 Evaluating the Causal Effect of an optimal ITR with Categorical Treatment

While the procedure is analogous to the previously described binary treatment, we now need to pay attention to the type of blip we define in the estimation stage, as well as how we construct our learners.

5.6.1.1 Simulated Data

  • First, we load the simulated data. Here, our data generating distribution was of the following form:

\[W \sim \mathcal{N}(\bf{0},I_{4 \times 4})\] \[P(A|W) = \frac{1}{1+\exp^{(-(0.05*I(A=1)*W_1+0.8*I(A=2)*W_1+0.8*I(A=3)*W_1))}}\]

\[P(Y|A,W) = 0.5\text{logit}^{-1}[15I(A=1)(W_1-0.5) - 3I(A=2)(2W_1+0.5) \\ + 3I(A=3)(3W_1-0.5)] +\text{logit}^{-1}(W_2W_1)\]

  • We can just load the data available as part of the package as follows:
  • The above composes our observed data structure \(O = (W, A, Y)\). Note that the mean under the true optimal rule is \(\psi=0.658\), which is the quantity we aim to estimate.

5.6.1.2 Constructing Optimal Stacked Regressions with sl3

QUESTION: With categorical treatment, what is the dimension of the blip now? How would we go about estimating it?

  • We generate three different ensemble learners that must be fit, corresponding to the learners for the outcome regression, propensity score, and the blip function.

  • Note that we need to estimate \(g_0(A|W)\) for a categorical \(A\)- therefore we use the multinomial Super Learner option available within the sl3 package with learners that can address multi-class classification problems.

  • In order to see which learners can be used to estimate \(g_0(A|W)\) in sl3, we run the following:

 [1] "Lrnr_bartMachine"           "Lrnr_caret"                
 [3] "Lrnr_dbarts"                "Lrnr_gam"                  
 [5] "Lrnr_glmnet"                "Lrnr_grf"                  
 [7] "Lrnr_h2o_glm"               "Lrnr_h2o_grid"             
 [9] "Lrnr_independent_binomial"  "Lrnr_mean"                 
[11] "Lrnr_multivariate"          "Lrnr_optim"                
[13] "Lrnr_polspline"             "Lrnr_pooled_hazards"       
[15] "Lrnr_randomForest"          "Lrnr_ranger"               
[17] "Lrnr_rpart"                 "Lrnr_screener_corP"        
[19] "Lrnr_screener_corRank"      "Lrnr_screener_randomForest"
[21] "Lrnr_solnp"                 "Lrnr_svm"                  
[23] "Lrnr_xgboost"

5.6.1.3 Targeted Estimation of the Mean under the Optimal Individualized Interventions Effects

A tmle3_Fit that took 1 step(s)
   type         param  init_est  tmle_est         se     lower     upper
1:  TSM E[Y_{A=NULL}] 0.5580952 0.6817778 0.05872254 0.5666837 0.7968718
   psi_transformed lower_transformed upper_transformed
1:       0.6817778         0.5666837         0.7968718

  1   2   3 
274 432 294

We can see that the confidence interval covers our true mean under the true optimal individualized treatment.

NOTICE the distribution of the assigned treatment! We will need this shortly.

5.7 Extensions to Causal Effect of an OIT

  • We consider two extensions to the procedure described for estimating the value of the ITR.

  • The first one considers a setting where the user might be interested in a grid of possible suboptimal rules, corresponding to potentially limited knowledge of potential effect modifiers (Simpler Rules).

  • The second extension concerns implementation of realistic optimal individual interventions where certain regimes might be preferred, but due to practical or global positivity restraints are not realistic to implement (Realistic Interventions).

5.7.1 Simpler Rules

  • In order to not only consider the most ambitious fully \(V\)-optimal rule, we define \(S\)-optimal rules as the optimal rule that considers all possible subsets of \(V\) covariates, with card(\(S\)) \(\leq\) card(\(V\)) and \(\emptyset \in S\).

  • This allows us to consider sub-optimal rules that are easier to estimate and potentially provide more realistic rules- as such, we allow for statistical inference for the counterfactual mean outcome under the sub-optimal rule.

A tmle3_Fit that took 1 step(s)
   type             param  init_est  tmle_est         se     lower     upper
1:  TSM E[Y_{A=W3,W2,W1}] 0.5411311 0.5719339 0.07002195 0.4346934 0.7091744
   psi_transformed lower_transformed upper_transformed
1:       0.5719339         0.4346934         0.7091744

Even though the user specified all baseline covariates as the basis for rule estimation, a simpler rule is sufficient to maximize the mean under the optimal individualized treatment!

QUESTION: Why do you think the estimate is higher under the less complex rule? How does the set of covariates picked by tmle3mopttx compare to the baseline covariates the true rule depends on?

5.7.2 Realistic Optimal Individual Regimes

  • tmle3mopttx also provides an option to estimate the mean under the realistic, or implementable, optimal individualized treatment.

  • It is often the case that assigning particular regime might have the ability to fully maximize (or minimize) the desired outcome, but due to global or practical positivity constrains, such treatment can never be implemented in real life (or is highly unlikely).

  • Specifying realistic="TRUE", we consider possibly suboptimal treatments that optimize the outcome in question while being supported by the data.

A tmle3_Fit that took 1 step(s)
   type         param  init_est  tmle_est        se     lower     upper
1:  TSM E[Y_{A=NULL}] 0.5509372 0.6617419 0.0212618 0.6200695 0.7034142
   psi_transformed lower_transformed upper_transformed
1:       0.6617419         0.6200695         0.7034142

  2   3 
508 492

QUESTION: Referring back to the data-generating distribution, why do you think the distribution of allocated treatment changed from the distribution that we had under the “non-realistic” rule?

5.7.3 Variable Importance Analysis

  • In the previous sections we have seen how to obtain a contrast between the mean under the optimal individualized rule and the mean under the observed outcome for a single covariate. We are now ready to run the variable importance analysis for all of our observed covariates!

  • In order to run tmle3mopttx variable importance measure, we need considered covariates to be categorical variables.

  • For illustration purpose, we bin baseline covariates corresponding to the data-generating distribution described in the previous section:

  • Note that our node list now includes \(W_1\) as treatments as well! Don’t worry, we will still properly adjust for all baseline covariates when considering \(A\) as treatment.

5.7.3.1 Variable Importance using Targeted Estimation of the value of the ITR

  • We will initialize a specification for the TMLE of our parameter of interest (called a tmle3_Spec in the tlverse nomenclature) simply by calling tmle3_mopttx_vim.
   type                  param     init_est    tmle_est         se       lower
1:   RR RR(E[Y_{A=NULL}]/E[Y]) -0.001196441  0.08955757 0.03342250  0.02405067
2:   RR RR(E[Y_{A=NULL}]/E[Y]) -0.026633542 -0.08544667 0.05070127 -0.18481932
        upper psi_transformed lower_transformed upper_transformed  A
1: 0.15506447       1.0936903         1.0243422          1.167733  A
2: 0.01392599       0.9181021         0.8312545          1.014023 W1
             W    Z_stat        p_nz p_nz_corrected
1: W3,W4,W2,W1  2.679559 0.003685958    0.007371915
2:  W3,W4,W2,A -1.685296 0.045965696    0.045965696

The final result of tmle3_vim with the tmle3mopttx spec is an ordered list of mean outcomes under the optimal individualized treatment for all categorical covariates in our dataset.

5.8 Exercise

5.8.1 Real World Data and tmle3mopttx

Finally, we cement everything we learned so far with a real data application.

As in the previous sections, we will be using the WASH Benefits data, corresponding to the Effect of water quality, sanitation, hand washing, and nutritional interventions on child development in rural Bangladesh trial.

The main aim of the cluster-randomized controlled trial was to assess the impact of six intervention groups, including:

  1. Control

  2. Handwashing with soap

  3. Improved nutrition through counselling and provision of lipid-based nutrient supplements

  4. Combined water, sanitation, handwashing, and nutrition.

  5. Improved sanitation

  6. Combined water, sanitation, and handwashing

  7. Chlorinated drinking water

We aim to estimate the optimal ITR and the corresponding value under the optimal ITR for the main intervention in WASH Benefits data!

Our outcome of interest is the weight-for-height Z-score, whereas our treatment is the six intervention groups aimed at improving living conditions.

Questions:

  1. Define \(V\) as mother’s education (momedu), current living conditions (floor), and possession of material items including the refrigerator (asset_refrig). Why do you think we use these covariates as \(V\)? Do we want to minimize or maximize the outcome? Which blip type should we use? Construct an appropriate sl3 library for \(A\), \(Y\) and \(B\).

  2. Based on the \(V\) defined in the previous question, estimate the mean under the ITR for the main randomized intervention used in the WASH Benefits trial with weight-for-height Z-score as the outcome. What’s the TMLE value of the optimal ITR? How does it change from the initial estimate? Which intervention is the most dominant? Why do you think that is?

  3. Using the same formulation as in questions 1 and 2, estimate the realistic optimal ITR and the corresponding value of the realistic ITR. Did the results change? Which intervention is the most dominant under realistic rules? Why do you think that is?

5.9 Summary

  • In summary, the mean outcome under the optimal individualized treatment is a counterfactual quantity of interest representing what the mean outcome would have been if everybody, contrary to the fact, received treatment that optimized their outcome.

  • tmle3mopttx estimates the mean outcome under the optimal individualized treatment, where the candidate rules are restricted to only respond to a user-supplied subset of the baseline and intermediate covariates. In addition it provides options for realistic, data-adaptive interventions.

  • In essence, our target parameter answers the key aim of precision medicine: allocating the available treatment by tailoring it to the individual characteristics of the patient, with the goal of optimizing the final outcome.

5.9.1 Solutions

To start, let’s load the data, convert all columns to be of class numeric, and take a quick look at it:

As before, we specify the NPSEM via the node_list object.

We pick few potential effect modifiers, including mother’s education, current living conditions (floor), and possession of material items including the refrigerator. We concentrate of these covariates as they might be indicative of the socio-economic status of individuals involved in the trial. We can explore the distribution of our \(V\), \(A\) and \(Y\):

We specify a simply library for the outcome regression, propensity score and the blip function. Since our treatment is categorical, we need to define a multinomial learner for \(A\) and multivariate learner for \(B\). We will define the xgboost over a grid of parameters, and initialize a mean learner.

As seen before, we initialize the tmle3_mopttx_blip_revere Spec in order to answer Question 1. We want to maximize our outcome, with higher the weight-for-height Z-score the better. We will also use blip2 as the blip type, but note that we could have used blip1 as well since “Control” is a good reference category.

Using the same formulation as before, we estimate the realistic optimal ITR and the corresponding value of the realistic ITR: