Chapter 6 Stochastic Treatment Regimes

Nima Hejazi

Based on the tmle3shift R package by Nima Hejazi, Jeremy Coyle, and Mark van der Laan.

Updated: 2020-02-20

6.1 Learning Objectives

  1. Differentiate stochastic treatment regimes from static, dynamic, and optimal treatment regimes.
  2. Describe how estimating causal effects of stochastic interventions informs a real-world data analysis.
  3. Contrast a population level stochastic intervention policy from a modified treatment policy.
  4. Estimate causal effects under stochastic treatment regimes with the tmle3shift R package.
  5. Specify a grid of counterfactual shift interventions to be used for defining a set of stochastic intervention policies.
  6. Interpret a set of effect estimates from a grid of counterfactual shift interventions.
  7. Construct marginal structural models to measure variable importance in terms of stochastic interventions, using a grid of shift interventions.
  8. Implement a shift intervention at the individual level, to facilitate shifting each individual to a value that’s supported by the data.
  9. Define novel shift intervention functions to extend the tmle3shift R package.

6.2 Introduction

In this section, we examine a simple example of stochastic treatment regimes in the context of a continuous treatment variable of interest, defining an intuitive causal effect through which to examine stochastic interventions more generally. As a first step to using stochastic treatment regimes in practice, we present the tmle3shift R package, which features an implementation of a recently developed algorithm for computing targeted minimum loss-based estimates of a causal effect based on a stochastic treatment regime that shifts the natural value of the treatment based on a shifting function \(d(A,W)\). We will also use tmle3shift to construct marginal structural models for variable importance measures, implement shift interventions at the individual level, and define novel shift intervention functions.

6.3 Stochastic Interventions

  • Present a relatively simple yet extremely flexible manner by which realistic causal effects (and contrasts thereof) may be defined.
  • May be applied to nearly any manner of treatment variable – continuous, ordinal, categorical, binary – allowing for a rich set of causal effects to be defined through this formalism.

  • Arguably the most general of the classes of interventions through which causal effects may be defined, and are conceptually simple.

  • We may consider stochastic interventions in two ways:

    1. The equation \(f_A\), which produces \(A\), is replaced by a probabilistic mechanism \(g_{\delta}(A \mid W)\) that differs from the original \(g(A \mid W)\). The stochastically modified value of the treatment \(A_{\delta}\) is drawn from a user-specified distribution \(g_\delta(A \mid W)\), which may depend on the original distribution \(g(A \mid W)\) and is indexed by a user-specified parameter \(\delta\). In this case, the stochastically modified value of the treatment \(A_{\delta} \sim g_{\delta}(\cdot \mid W)\).

    2. The observed value \(A\) is replaced by a new value \(A_{d(A,W)}\) based on applying a user-defined function \(d(A,W)\) to \(A\). In this case, the stochastic treatment regime may be viewed as an intervention in which \(A\) is set equal to a value based on a hypothetical regime \(d(A, W)\), where regime \(d\) depends on the treatment level \(A\) that would be assigned in the absence of the regime as well as the covariates \(W\). Stochastic interventions of this variety may be referred to as depending on the natural value of treatment or as modified treatment policies (Haneuse and Rotnitzky 2013; Young, Hernán, and Robins 2014).

6.3.1 Identifying the Causal Effect of a Stochastic Intervention

  • The stochastic intervention generates a counterfactual random variable \(Y_{d(A,W)} := f_Y(d(A,W), W, U_Y) \equiv Y_{g_{\delta}} := f_Y(A_{\delta}, W, U_Y)\), where \(Y_{d(A,W)} \sim \mathcal{P}_0^{\delta}\).

  • The target causal estimand of our analysis is \(\psi_{0, \delta} := \mathbb{E}_{P_0^{\delta}}\{Y_{d(A,W)}\}\), the mean of the counterfactual outcome variable \(Y_{d(A, W)}\). The statistical target parameter may also be denoted \(\Psi(P_0) = \mathbb{E}_{P_0}{\overline{Q}(d(A, W), W)}\), where \(\overline{Q}(d(A, W), W)\) is the counterfactual outcome value of a given individual under the stochastic intervention distribution (Díaz and van der Laan 2018).

  • In prior work, Díaz and van der Laan (2012) showed that the causal quantity of interest \(\mathbb{E}_0 \{Y_{d(A, W)}\}\) is identified by a functional of the distribution of \(O\): \[\begin{align*}\label{eqn:identification2012} \psi_{0,d} = \int_{\mathcal{W}} \int_{\mathcal{A}} & \mathbb{E}_{P_0} \{Y \mid A = d(a, w), W = w\} \cdot \\ &q_{0, A}^O(a \mid W = w) \cdot q_{0, W}^O(w) d\mu(a)d\nu(w). \end{align*}\]

  • The four standard assumptions presented in are necessary in order to establish identifiability of the causal parameter from the observed data via the statistical functional. These were

    1. Consistency: \(Y^{d(a_i, w_i)}_i = Y_i\) in the event \(A_i = d(a_i, w_i)\), for \(i = 1, \ldots, n\)
    2. Stable unit value treatment assumption (SUTVA): \(Y^{d(a_i, w_i)}_i\) does not depend on \(d(a_j, w_j)\) for \(i = 1, \ldots, n\) and \(j \neq i\), or lack of interference (Rubin 1978, 1980).
    3. Strong ignorability: \(A_i \perp \!\!\! \perp Y^{d(a_i, w_i)}_i \mid W_i\), for \(i = 1, \ldots, n\).
    4. Positivity (or overlap): \(a_i \in \mathcal{A} \implies d(a_i, w_i) \in \mathcal{A}\) for all \(w \in \mathcal{W}\), where \(\mathcal{A}\) denotes the support of \(A \mid W = w_i \quad \forall i = 1, \ldots n\).

  • With the identification assumptions satisfied, Díaz and van der Laan (2012) and Díaz and van der Laan (2018) provide an efficient influence function with respect to the nonparametric model \(\mathcal{M}\) as \[\begin{equation*}\label{eqn:eif} D(P_0)(x) = H(a, w)({y - \overline{Q}(a, w)}) + \overline{Q}(d(a, w), w) - \Psi(P_0), \end{equation*}\] where the auxiliary covariate \(H(a,w)\) may be expressed \[\begin{equation*}\label{eqn:aux_covar_full} H(a,w) = \mathbb{I}(a + \delta < u(w)) \frac{g_0(a - \delta \mid w)} {g_0(a \mid w)} + \mathbb{I}(a + \delta \geq u(w)), \end{equation*}\] which may be reduced to \[\begin{equation*}\label{eqn:aux_covar_simple} H(a,w) = \frac{g_0(a - \delta \mid w)}{g_0(a \mid w)} + 1 \end{equation*}\] in the case that the treatment is in the limits that arise from conditioning on \(W\), i.e., for \(A_i \in (u(w) - \delta, u(w))\).

6.3.2 Interpreting the Causal Effect of a Stochastic Intervention

Animation of how a counterfactual outcome changes as the natural treatment distribution is subjected to a simple stochastic intervention

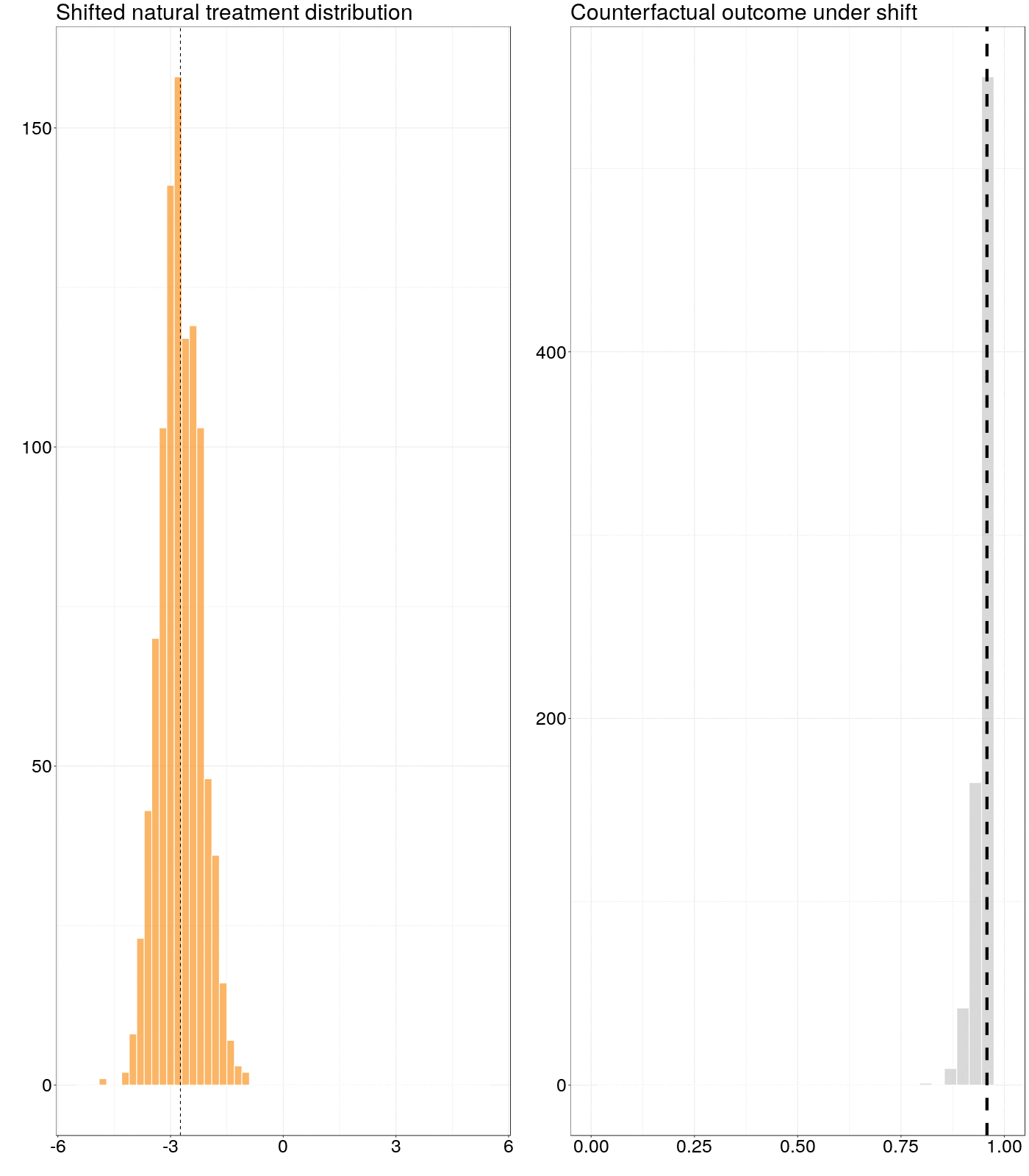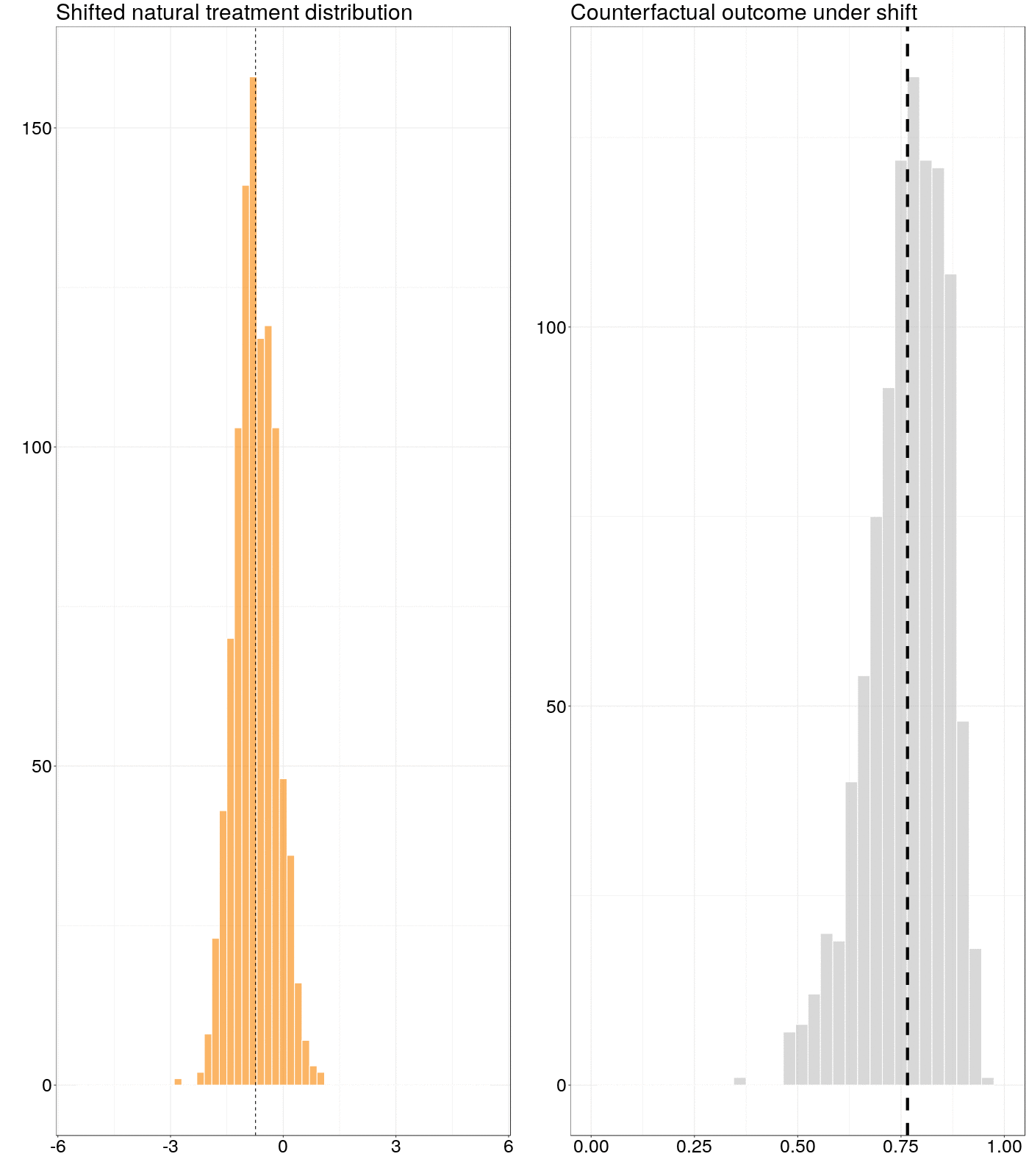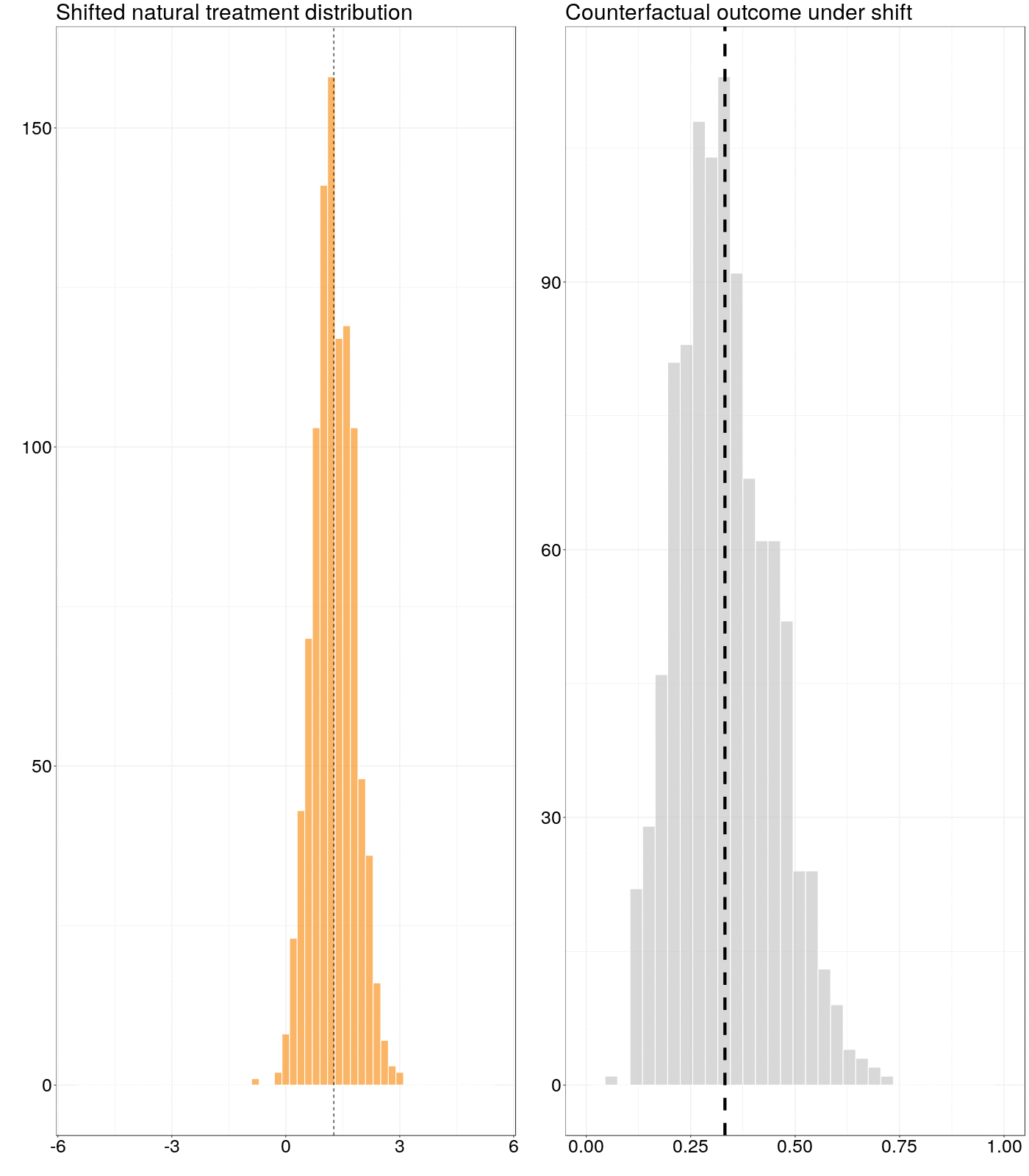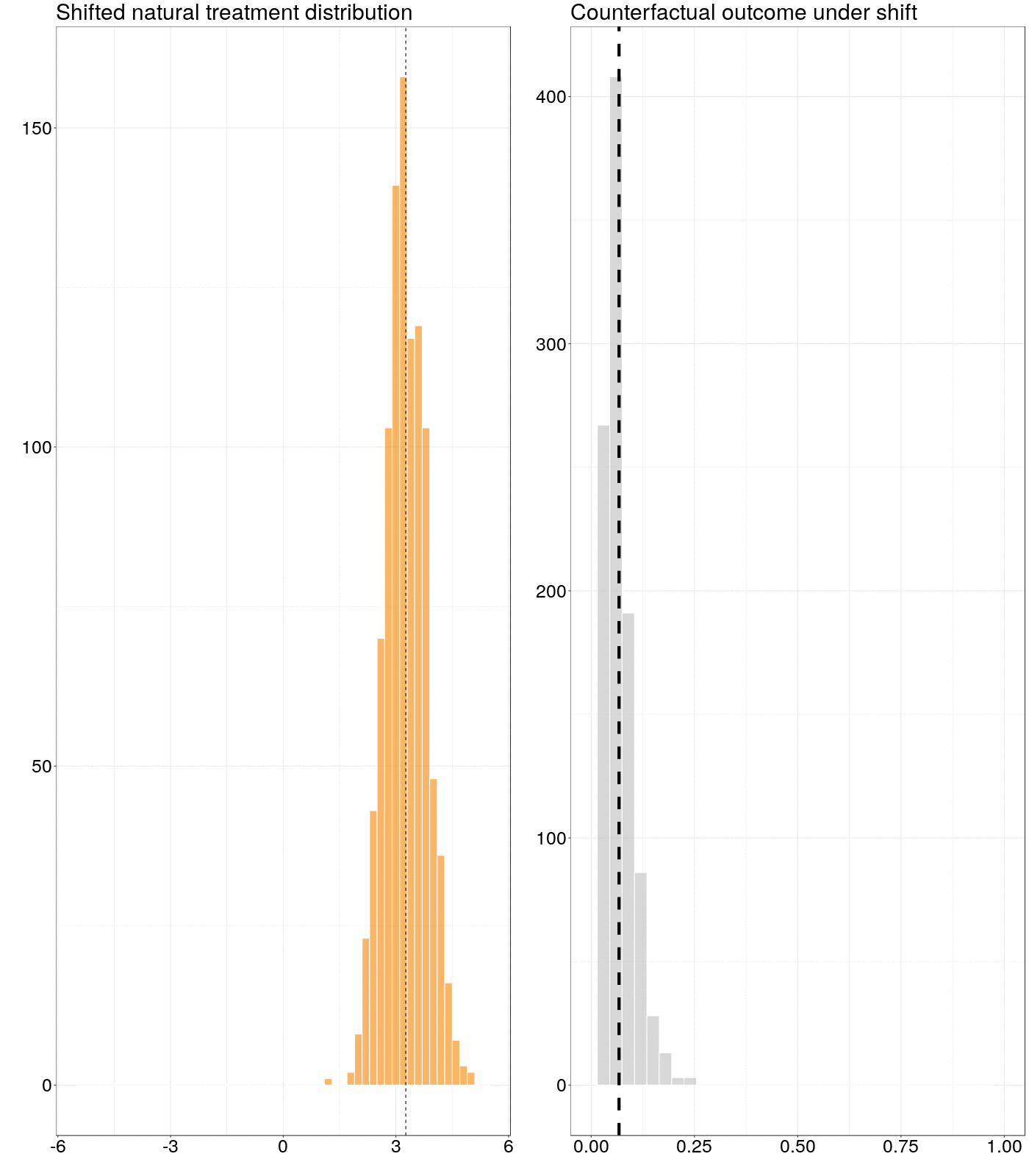
Figure 6.1: Animation of how a counterfactual outcome changes as the natural treatment distribution is subjected to a simple stochastic intervention

6.4 Estimating the Causal Effect of a Stochastic Intervention with tmle3shift

We use tmle3shift to construct a targeted maximum likelihood (TML) estimator of of a causal effect of a stochastic treatment regime that shifts the natural value of the treatment based on a shifting function \(d(A,W)\). We will follow the recipe provided by Díaz and van der Laan (2018), tailored to the tmle3 framework:

  1. Construct initial estimators \(g_n\) of \(g_0(A, W)\) and \(Q_n\) of \(\overline{Q}_0(A, W)\), perhaps using data-adaptive regression techniques.
  2. For each observation \(i\), compute an estimate \(H_n(a_i, w_i)\) of the auxiliary covariate \(H(a_i,w_i)\).
  3. Estimate the parameter \(\epsilon\) in the logistic regression model \[ \text{logit}\overline{Q}_{\epsilon, n}(a, w) = \text{logit}\overline{Q}_n(a, w) + \epsilon H_n(a, w),\] or an alternative regression model incorporating weights.
  4. Compute TML estimator \(\Psi_n\) of the target parameter, defining update \(\overline{Q}_n^{\star}\) of the initial estimate \(\overline{Q}_{n, \epsilon_n}\): \[\begin{equation*}\label{eqn:tmle} \Psi_n = \Psi(P_n^{\star}) = \frac{1}{n} \sum_{i = 1}^n \overline{Q}_n^{\star}(d(A_i, W_i), W_i). \end{equation*}\]

To start, let’s load the packages we’ll use and set a seed for simulation:

1. Construct initial estimators \(g_n\) of \(g_0(A, W)\) and \(Q_n\) of \(\overline{Q}_0(A, W)\).

We need to estimate two components of the likelihood in order to construct a TML estimator.

  1. The outcome regression, \(\hat{Q}_n\), which is a simple regression of the form \(\mathbb{E}[Y \mid A,W]\).
  1. The treatment mechanism, \(\hat{g}_n\), i.e., the propensity score. In the case of a continuous intervention, such a quantity is a conditional density. Generally speaking, conditional density estimation is a challenging problem that has received much attention in the literature. To estimate the treatment mechanism, we must make use of learning algorithms specifically suited to conditional density estimation; a list of such learners may be extracted from sl3 by using sl3_list_learners():
[1] "Lrnr_condensier"             "Lrnr_density_discretize"    
[3] "Lrnr_density_hse"            "Lrnr_density_semiparametric"
[5] "Lrnr_haldensify"             "Lrnr_rfcde"                 
[7] "Lrnr_solnp_density"

To proceed, we’ll select two of the above learners, Lrnr_haldensify for using the highly adaptive lasso for conditional density estimation, based on an algorithm given by Díaz and van der Laan (2011) and implemented in Hejazi and Benkeser (2019), and Lrnr_rfcde, an approach for using random forests for conditional density estimation (Pospisil and Lee 2018). A Super Learner may be constructed by pooling estimates from each of these modified conditional density regression techniques.

Finally, we construct a learner_list object for use in constructing a TML estimator of our target parameter of interest:

6.4.1 Simulate Data

   W1 W2          A Y
1:  1  1  3.5806529 1
2:  1  0  3.2071846 1
3:  1  1  1.0358382 1
4:  0  0 -0.6578495 1
5:  1  1  3.0199033 1
6:  1  1  2.7803127 1

We now have an observed data structure (data) and a specification of the role that each variable in the data set plays as the nodes in a directed acyclic graph (DAG) via nonparametric structural equation models (NPSEMs).

To start, we will initialize a specification for the TMLE of our parameter of interest (a tmle3_Spec in the tlverse nomenclature) simply by calling tmle_shift. We specify the argument shift_val = 0.5 when initializing the tmle3_Spec object to communicate that we’re interested in a shift of \(0.5\) on the scale of the treatment \(A\) – that is, we specify \(\delta = 0.5\).

As seen above, the tmle_shift specification object (like all tmle3_Spec objects) does not store the data for our specific analysis of interest. Later, we’ll see that passing a data object directly to the tmle3 wrapper function, alongside the instantiated tmle_spec, will serve to construct a tmle3_Task object internally (see the tmle3 documentation for details).

Note that in the initialization of the tmle3_Spec, we specified a shifting function shift_additive_bounded (and its inverse). This shifting function corresponds to a stochastic regime slightly more complicated than that initially considered in Díaz and van der Laan (2018). In particular, shift_additive_bounded is encapsulates a procedure that determines an acceptable set of shifting values for the shift \(\delta\), allowing for the observed treatment value of a given observation to be shifted if the auxiliary covariate \(H_n\) is bounded by a constant and not shifting the given observation if this criterion does not hold. We discuss this in greater detail in the sequel.

6.4.2 Targeted Estimation of Stochastic Interventions Effects


Iter: 1 fn: 1374.2507    Pars:  0.80530 0.19470
Iter: 2 fn: 1374.2507    Pars:  0.80531 0.19469
solnp--> Completed in 2 iterations
A tmle3_Fit that took 1 step(s)
   type         param  init_est tmle_est         se     lower     upper
1:  TSM E[Y_{A=NULL}] 0.7949624 0.796194 0.01232561 0.7720363 0.8203518
   psi_transformed lower_transformed upper_transformed
1:        0.796194         0.7720363         0.8203518

The print method of the resultant tmle_fit object conveniently displays the results from computing our TML estimator.

6.5 Stochastic Interventions over a Grid of Counterfactual Shifts

  • Consider an arbitrary scalar \(\delta\) that defines a counterfactual outcome \(\psi_n = Q_n(d(A, W), W)\), where, for simplicity, let \(d(A, W) = A + \delta\). A simplified expression of the auxiliary covariate for the TMLE of \(\psi\) is \(H_n = \frac{g^{\star}(a \mid w)}{g(a \mid w)}\), where \(g^{\star}(a \mid w)\) defines the treatment mechanism with the stochastic intervention implemented. In this manner, we can specify a grid of shifts \(\delta\) to define a set of stochastic intervention policies in an a priori manner.

  • To ascertain whether a given choice of the shift \(\delta\) is acceptable, let there be a bound \(C(\delta) = \frac{g^{\star}(a \mid w)}{g(a \mid w)} \leq M\), where \(g^{\star}(a \mid w)\) is a function of \(\delta\) in part, and \(M\) is a user-specified upper bound of \(C(\delta)\). Then, \(C(\delta)\) is a measure of the influence of a given observation (under a bound of the ratio of the conditional densities), which provides a way to limit the maximum influence of a given observation through a choice of the shift \(\delta\).

  • For the purpose of using such a shift in practice, the present software provides the functions shift_additive_bounded and shift_additive_bounded_inv, which define a variation of this shift: \[\begin{equation} \delta(a, w) = \begin{cases} \delta, & C(\delta) \leq M \\ 0, \text{otherwise} \\ \end{cases}, \end{equation}\] which corresponds to an intervention in which the natural value of treatment of a given observational unit is shifted by a value \(\delta\) in the case that the ratio of the intervened density \(g^{\star}(a \mid w)\) to the natural density \(g(a \mid w)\) (that is, \(C(\delta)\)) does not exceed a bound \(M\). In the case that the ratio \(C(\delta)\) exceeds the bound \(M\), the stochastic intervention policy does not apply to the given unit and they remain at their natural value of treatment \(a\).

6.5.1 Initializing vimshift through its tmle3_Spec

To start, we will initialize a specification for the TMLE of our parameter of interest (called a tmle3_Spec in the tlverse nomenclature) simply by calling tmle_shift. We specify the argument shift_grid = seq(-1, 1, by = 1) when initializing the tmle3_Spec object to communicate that we’re interested in assessing the mean counterfactual outcome over a grid of shifts -1, 0, 1 on the scale of the treatment \(A\).

6.5.2 Targeted Estimation of Stochastic Intervention Effects

One may walk through the step-by-step procedure for fitting the TML estimator of the mean counterfactual outcome under each shift in the grid, using the machinery exposed by the tmle3 R package, or simply invoke the tmle3 wrapper function to fit the series of TML estimators (one for each parameter defined by the grid delta) in a single function call. For convenience, we choose the latter:


Iter: 1 fn: 1379.6096    Pars:  0.77181 0.22819
Iter: 2 fn: 1379.6096    Pars:  0.77181 0.22819
solnp--> Completed in 2 iterations
A tmle3_Fit that took 1 step(s)
         type          param  init_est  tmle_est          se     lower
1:        TSM  E[Y_{A=NULL}] 0.6258642 0.6257461 0.014135823 0.5980404
2:        TSM  E[Y_{A=NULL}] 0.7385594 0.7390000 0.013895038 0.7117662
3:        TSM  E[Y_{A=NULL}] 0.8437586 0.8467042 0.010062320 0.8269824
4: MSM_linear MSM(intercept) 0.7360607 0.7371501 0.012189075 0.7132599
5: MSM_linear     MSM(slope) 0.1089472 0.1104791 0.004285835 0.1020790
       upper psi_transformed lower_transformed upper_transformed
1: 0.6534518       0.6257461         0.5980404         0.6534518
2: 0.7662338       0.7390000         0.7117662         0.7662338
3: 0.8664260       0.8467042         0.8269824         0.8664260
4: 0.7610402       0.7371501         0.7132599         0.7610402
5: 0.1188791       0.1104791         0.1020790         0.1188791

Remark: The print method of the resultant tmle_fit object conveniently displays the results from computing our TML estimator.

6.5.3 Inference with Marginal Structural Models

Since we consider estimating the mean counterfactual outcome \(\psi_n\) under several values of the intervention \(\delta\), taken from the aforementioned \(\delta\)-grid, one approach for obtaining inference on a single summary measure of these estimated quantities involves leveraging working marginal structural models (MSMs). Summarizing the estimates \(\psi_n\) through a working MSM allows for inference on the trend imposed by a \(\delta\)-grid to be evaluated via a simple hypothesis test on a parameter of this working MSM. Letting \(\psi_{\delta}(P_0)\) be the mean outcome under a shift \(\delta\) of the treatment, we have \(\vec{\psi}_{\delta} = (\psi_{\delta}: \delta)\) with corresponding estimators \(\vec{\psi}_{n, \delta} = (\psi_{n, \delta}: \delta)\). Further, let \(\beta(\vec{\psi}_{\delta}) = \phi((\psi_{\delta}: \delta))\). By a straightforward application of the delta method (discussed previously), we may write the efficient influence function of the MSM parameter \(\beta\) in terms of the EIFs of each of the corresponding point estimates. Based on this, inference from a working MSM is rather straightforward. To wit, the limiting distribution for \(m_{\beta}(\delta)\) may be expressed \[\sqrt{n}(\beta_n - \beta_0) \to N(0, \Sigma),\] where \(\Sigma\) is the empirical covariance matrix of \(\text{EIF}_{\beta}(O)\).

         type          param  init_est  tmle_est          se     lower
1: MSM_linear MSM(intercept) 0.7360607 0.7371501 0.012189075 0.7132599
2: MSM_linear     MSM(slope) 0.1089472 0.1104791 0.004285835 0.1020790
       upper psi_transformed lower_transformed upper_transformed
1: 0.7610402       0.7371501         0.7132599         0.7610402
2: 0.1188791       0.1104791         0.1020790         0.1188791

6.5.4 Directly Targeting the MSM Parameter \(\beta\)

Note that in the above, a working MSM is fit to the individual TML estimates of the mean counterfactual outcome under a given value of the shift \(\delta\) in the supplied grid. The parameter of interest \(\beta\) of the MSM is asymptotically linear (and, in fact, a TML estimator) as a consequence of its construction from individual TML estimators. In smaller samples, it may be prudent to perform a TML estimation procedure that targets the parameter \(\beta\) directly, as opposed to constructing it from several independently targeted TML estimates. An approach for constructing such an estimator is proposed in the sequel.

Suppose a simple working MSM \(\mathbb{E}Y_{g^0_{\delta}} = \beta_0 + \beta_1 \delta\), then a TML estimator targeting \(\beta_0\) and \(\beta_1\) may be constructed as \[\overline{Q}_{n, \epsilon}(A,W) = \overline{Q}_n(A,W) + \epsilon (H_1(g), H_2(g),\] for all \(\delta\), where \(H_1(g)\) is the auxiliary covariate for \(\beta_0\) and \(H_2(g)\) is the auxiliary covariate for \(\beta_1\).

To construct a targeted maximum likelihood estimator that directly targets the parameters of the working marginal structural model, we may use the tmle_vimshift_msm Spec (instead of the tmle_vimshift_delta Spec that appears above):


Iter: 1 fn: 1377.3851    Pars:  0.78792 0.21208
Iter: 2 fn: 1377.3851    Pars:  0.78792 0.21208
solnp--> Completed in 2 iterations
A tmle3_Fit that took 1 step(s)
         type          param  init_est  tmle_est          se     lower
1: MSM_linear MSM(intercept) 0.7368292 0.7371626 0.012336497 0.7129835
2: MSM_linear     MSM(slope) 0.1073148 0.1073468 0.004654671 0.0982238
       upper psi_transformed lower_transformed upper_transformed
1: 0.7613417       0.7371626         0.7129835         0.7613417
2: 0.1164698       0.1073468         0.0982238         0.1164698

6.5.5 Example with the WASH Benefits Data

To complete our walk through, let’s turn to using stochastic interventions to investigate the data from the WASH Benefits trial. To start, let’s load the data, convert all columns to be of class numeric, and take a quick look at it

     whz          tr fracode month aged    sex momage         momedu momheight
1: -0.94 Handwashing  N06505     7  237   male     21 Primary (1-5y)    146.00
2: -1.13     Control  N06505     8  310 female     26   No education    148.90
3: -1.61     Control  N06524     3  162   male     25 Primary (1-5y)    153.75
       hfiacat Nlt18 Ncomp watmin elec floor walls roof asset_wardrobe
1: Food Secure     1    25      2    1     0     1    1              0
2: Food Secure     1     7      4    1     0     0    1              0
3: Food Secure     0    15      2    0     0     1    1              0
   asset_table asset_chair asset_khat asset_chouki asset_tv asset_refrig
1:           1           0          0            1        0            0
2:           1           1          0            1        0            0
3:           1           0          1            1        0            0
   asset_bike asset_moto asset_sewmach asset_mobile
1:          0          0             0            0
2:          0          0             0            1
3:          0          0             0            0

Next, we specify our NPSEM via the node_list object. For our example analysis, we’ll consider the outcome to be the weight-for-height Z-score (as in previous sections), the intervention of interest to be the mother’s age at time of child’s birth, and take all other covariates to be potential confounders.

Were we to consider the counterfactual weight-for-height Z-score under shifts in the age of the mother at child’s birth, how would we interpret estimates of our parameter?

To simplify our interpretation, consider a shift (up or down) of two years in the mother’s age (i.e., \(\delta = \{-2, 0, 2\}\)); in this setting, a stochastic intervention would correspond to a policy advocating that potential mothers defer or accelerate plans of having a child for two calendar years, possibly implemented through the deployment of an encouragement design.

First, let’s try a simple upward shift of just two years:

To examine the effect modification approach we looked at in previous chapters, we’ll estimate the effect of this shift \(\delta = 2\) while stratifying on the mother’s education level (momedu, a categorical variable with three levels). For this, we augment our initialized tmle3_Spec object like so

Prior to running our analysis, we’ll modify the learner_list object we had created such that the density estimation procedure we rely on will be only the random forest conditional density estimation procedure of Pospisil and Lee (2018), as the nonparametric conditional density approach based on the highly adaptive lasso (Díaz and van der Laan 2011; Benkeser and van der Laan 2016; Coyle and Hejazi 2018; Hejazi and Benkeser 2019) is currently unable to accommodate large datasets.

Now we’re ready to construct a TML estimate of the shift parameter at \(\delta = 2\), stratified across levels of our variable of interest:

A tmle3_Fit that took 1 step(s)
             type                             param   init_est   tmle_est
1:            TSM                     E[Y_{A=NULL}] -0.5671449 -0.5640067
2: stratified TSM  E[Y_{A=NULL}] | V=Primary (1-5y) -0.6159012 -0.6287840
3: stratified TSM    E[Y_{A=NULL}] | V=No education -0.6781456 -0.8867310
4: stratified TSM E[Y_{A=NULL}] | V=Secondary (>5y) -0.5046408 -0.4300195
           se      lower      upper psi_transformed lower_transformed
1: 0.05464803 -0.6711149 -0.4568985      -0.5640067        -0.6711149
2: 0.09357539 -0.8121885 -0.4453796      -0.6287840        -0.8121885
3: 0.16775830 -1.2155312 -0.5579308      -0.8867310        -1.2155312
4: 0.07043565 -0.5680708 -0.2919682      -0.4300195        -0.5680708
   upper_transformed
1:        -0.4568985
2:        -0.4453796
3:        -0.5579308
4:        -0.2919682

For the next example, we’ll use the variable importance strategy of considering a grid of stochastic interventions to evaluate the weight-for-height Z-score under a shift in the mother’s age down by two years (\(\delta = -2\)) through up by two years (\(\delta = 2\)), incrementing by a single year between the two. To do this, we simply initialize a Spec tmle_vimshift_delta similar to how we did in a previous example:

Having made the above preparations, we’re now ready to estimate the counterfactual mean of the weight-for-height Z-score under a small grid of shifts in the mother’s age at child’s birth. Just as before, we do this through a simple call to our tmle3 wrapper function:

A tmle3_Fit that took 1 step(s)
         type          param    init_est     tmle_est          se        lower
1:        TSM  E[Y_{A=NULL}] -0.55925245 -0.569402067 0.041952795 -0.651628036
2:        TSM  E[Y_{A=NULL}] -0.56188582 -0.549250780 0.044829591 -0.637115164
3:        TSM  E[Y_{A=NULL}] -0.56420938 -0.565294118 0.046631440 -0.656690060
4:        TSM  E[Y_{A=NULL}] -0.56599296 -0.522073719 0.047393545 -0.614963360
5:        TSM  E[Y_{A=NULL}] -0.56844858 -0.556455652 0.048241912 -0.651008062
6: MSM_linear MSM(intercept) -0.56395784 -0.552495267 0.044106684 -0.638942780
7: MSM_linear     MSM(slope) -0.00224994  0.005306989 0.007269758 -0.008941474
         upper psi_transformed lower_transformed upper_transformed
1: -0.48717610    -0.569402067      -0.651628036       -0.48717610
2: -0.46138640    -0.549250780      -0.637115164       -0.46138640
3: -0.47389818    -0.565294118      -0.656690060       -0.47389818
4: -0.42918408    -0.522073719      -0.614963360       -0.42918408
5: -0.46190324    -0.556455652      -0.651008062       -0.46190324
6: -0.46604775    -0.552495267      -0.638942780       -0.46604775
7:  0.01955545     0.005306989      -0.008941474        0.01955545

6.6 Exercises

  1. Set the sl3 library of algorithms for the Super Learner to a simple, interpretable library and use this new library to estimate the counterfactual mean of mother’s age at child’s birth (momage) under a shift \(\delta = 0\). What does this counterfactual mean equate to in terms of the observed data?

  2. Describe two (equivalent) ways in which the causal effects of stochastic interventions may be interpreted.

  3. Using a grid of values of the shift parameter \(\delta\) (e.g., \(\{-1, 0, +1\}\)), repeat the analysis on the variable of interest (momage), summarizing the trend for this sequence of shifts using a marginal structural model.

  4. For either the grid of shifts in the example preceding the exercises or that estimated in (3) above, plot the resultant estimates against their respective counterfactual shifts. Graphically add to the scatterplot a line with slope and intercept equivalent to the MSM fit through the individual TML estimates.

  5. How does the marginal structural model we used to summarize the trend along the sequence of shifts previously help to contextualize the estimated effect for a single shift? That is, how does access to estimates across several shifts and the marginal structural model parameters allow us to more richly interpret our findings?

References

Benkeser, David, and Mark J van der Laan. 2016. “The Highly Adaptive Lasso Estimator.” In 2016 IEEE International Conference on Data Science and Advanced Analytics (DSAA). IEEE. https://doi.org/10.1109/dsaa.2016.93.

Coyle, Jeremy R, and Nima S Hejazi. 2018. “hal9001: The Scalable Highly Adaptive LASSO.” https://github.com/tlverse/hal9001.

Díaz, Iván, and Mark J van der Laan. 2011. “Super Learner Based Conditional Density Estimation with Application to Marginal Structural Models.” The International Journal of Biostatistics 7 (1). De Gruyter: 1–20.

Díaz, Iván, and Mark J van der Laan. 2012. “Population Intervention Causal Effects Based on Stochastic Interventions.” Biometrics 68 (2). Wiley Online Library: 541–49.

Díaz, Iván, and Mark J van der Laan. 2018. “Stochastic Treatment Regimes.” In Targeted Learning in Data Science: Causal Inference for Complex Longitudinal Studies, 167–80. Springer Science & Business Media.

Haneuse, Sebastian, and Andrea Rotnitzky. 2013. “Estimation of the Effect of Interventions That Modify the Received Treatment.” Statistics in Medicine 32 (30). Wiley Online Library: 5260–77.

Hejazi, Nima S, and David C Benkeser. 2019. haldensify: Nonparametric Conditional Density Estimation with the Highly Adaptive Lasso in R. https://github.com/nhejazi/haldensify.

Pospisil, Taylor, and Ann B Lee. 2018. “RFCDE: Random Forests for Conditional Density Estimation.” arXiv Preprint arXiv:1804.05753.

Rubin, Donald B. 1978. “Bayesian Inference for Causal Effects: The Role of Randomization.” The Annals of Statistics. JSTOR, 34–58.

Rubin, Donald B. 1980. “Randomization Analysis of Experimental Data: The Fisher Randomization Test Comment.” Journal of the American Statistical Association 75 (371). JSTOR: 591–93.

Young, Jessica G, Miguel A Hernán, and James M Robins. 2014. “Identification, Estimation and Approximation of Risk Under Interventions That Depend on the Natural Value of Treatment Using Observational Data.” Epidemiologic Methods 3 (1). De Gruyter: 1–19.