\(\DeclareMathOperator{\expit}{expit}\) \(\DeclareMathOperator{\logit}{logit}\) \(\DeclareMathOperator*{\argmin}{\arg\!\min}\) \(\newcommand{\indep}{\perp\!\!\!\perp}\) \(\newcommand{\coloneqq}{\mathrel{=}}\) \(\newcommand{\R}{\mathbb{R}}\) \(\newcommand{\E}{\mathbb{E}}\) \(\newcommand{\M}{\mathcal{M}}\) \(\renewcommand{\P}{\mathbb{P}}\) \(\newcommand{\I}{\mathbb{I}}\) \(\newcommand{\1}{\mathbbm{1}}\)
Skip to main content

Targeted Machine Learning with Big Data in the tlverse: A Short Course for the Public Health and Epidemiology Program (PASPE) at the National Institute of Public Health in Mexico

2 The Roadmap for Targeted Learning

Learning Objectives

By the end of this chapter you will be able to:

  • Follow the roadmap of targeted learning to translate meaningful research questions into realistic statistical estimation problems, and obtain valid inference in terms of confidence intervals and p-values.

Introduction

The roadmap of statistical learning is concerned with the translation from real-world data applications to a mathematical and statistical formulation of the relevant estimation problem. This involves data as a random variable having a probability distribution, scientific knowledge represented by a statistical model, a statistical target parameter representing an answer to the question of interest, and the notion of an estimator and sampling distribution of the estimator.

2.1 The Roadmap

The roadmap is a five-stage process of defining the following.

  1. Data as a random variable with a probability distribution, \(O \sim P_0\).
  2. The statistical model \(\M\) such that \(P_0 \in \M\).
  3. The statistical target parameter \(\Psi\) and estimand \(\Psi(P_0)\).
  4. The estimator \(\hat{\Psi}\) and estimate \(\hat{\Psi}(P_n)\).
  5. A measure of uncertainty for the estimate \(\hat{\Psi}(P_n)\).

(1) Data: A random variable with a probability distribution, \(O \sim P_0\)

The data set we are confronted with is the collection of the results of an experiment, and we can view the data as a random variable — that is, if we were to repeat the experiment, we would have a different realization of the data generated by the experiment in question. In particular, if the experiment were repeated many times, the probability distribution generating the data, \(P_0\), could be learned. So, the observed data on a single unit, \(O\), may be thought of as being drawn from a probability distribution \(P_0\). Most often, we observe \(n\) independent identically distributed (i.i.d.) observations of the random variable \(O\), so the observed data is the collection \(O_1, \ldots, O_n\), where the subscripts denote the individual observational units. While not all data are i.i.d., this is certainly the most common case in applied data analysis; moreover, there are a number of techniques for handling non-i.i.d. data, such as establishing conditional independence, stratifying data to create distinct sets of identically distributed data, and inferential corrections for repeated or clustered observations, to name but a few.

It is crucial that the domain scientist (i.e., researcher) have absolute clarity about what is actually known about the data-generating distribution for a given problem of interest. Just as critical is that this scientific information be communicated to the statistician, whose job it is to use such knowledge to guide any assumptions encoded in the choice of statistical model. Unfortunately, communication between statisticians and researchers is often fraught with misinterpretation. The roadmap provides a mechanism by which to ensure clear communication between the researcher and the statistician — it is an invaluable tool for such communication!

The empirical probability measure, \(P_n\)

With \(n\) i.i.d. observations in hand, we can define an empirical probability measure, \(P_n\). The empirical probability measure is an approximation of the true probability measure, \(P_0\), allowing us to learn from the observed data. For example, we can define the empirical probability measure of a set \(X\) to be the proportion of observations that belong in \(X\). That is, \[\begin{equation*} P_n(X) = \frac{1}{n}\sum_{i=1}^{n} \I(O_i \in X) \end{equation*}\]

In order to start learning from the data, we next need to ask “What do we know about the probability distribution of the data?” This brings us on to Step 2.

(2) Defining the statistical model \(\M\) such that \(P_0 \in \M\)

The statistical model \(\M\) is defined by the question we asked at the end of Step 1. It is the set of possible probability distributions that could describe our observed data, appropriately constrained by background scientific knowledge. Often \(\M\) is very large (e.g., nonparametric), reflecting the fact that statistical knowledge about the data-generating process is limited.

Alternatively, if the probability distribution of the data at hand is described by a finite number of parameters, then the statistical model is referred to as parametric. Such an assumption is made, for example, by the proposition that the random variable of interest, \(O\), has a normal distribution with mean \(\mu\) and variance \(\sigma^2\). More generally, a parametric model may be defined as

\[\begin{equation*} \M = \{P_{\theta} : \theta \in \R^d \}, \end{equation*}\] which describes a statistical model consisting of all distributions \(P_{\theta}\), that is all distributions indexed only by the parameter \(\theta\).

The assumption that the data-generating distribution has a specific, parametric form is made quite commonly, even when such assumptions are not supported by existing knowledge. This practice of oversimplification in the current culture of data analysis typically complicates any attempt at trying to answer the scientific question at hand, owing to the fact that possible model misspecification introduces bias of unknown magnitude. The philosophy used to justify such parametric assumptions is captured by the quote of George Box that “All models are wrong but some are useful,” which encourages the data analyst to make arbitrary modeling choices. The result is a practice of data science that often yields starkly different answers to the same scientific problem, due to the differing modeling decisions and assumptions made by different analysts. Even in the nascent days of data analysis, it was recognized that it is “far better [to develop] an approximate answer to the right question…than an exact answer to the wrong question, which can always be made precise” (Tukey 1962), though traditional statistics failed to heed this advice for a number of decades (Donoho 2017). The Targeted Learning paradigm avoids this bias by defining the statistical model through a representation of the true data-generating distribution corresponding to the observed data. The ultimate goal is to formulate the statistical estimation problem exactly, so that one can then set out to tailor to the problem the best possible estimation procedure.

Now, on to Step 3: “What are we trying to learn from the data?”

(3) The statistical target parameter \(\Psi\) and estimand \(\Psi(P_0)\)

The statistical target parameter, \(\Psi\), is defined as a mapping from the statistical model, \(\M\), to the parameter space (i.e., a real number) \(\R\) — that is, the target parameter is the mapping \(\Psi: \M \rightarrow \R\). The estimand may be seen as a representation of the quantity that we wish to learn from the data, the answer to a well-specified (often causal) question of interest. In contrast to purely statistical estimands, causal estimands require identification from the observed data, based on causal models that include several untestable assumptions, described in greater detail in the section on causal target parameters.

For a simple example, consider a data set which contains observations of a survival time on every subject, for which our question of interest is “What’s the probability that someone lives longer than five years?” We have,

\[\begin{equation*} \Psi(P_0) = \P_O(O > 5) = \int_5^{\infty} dP_O(o) \end{equation*}\]

This answer to this question is the estimand, \(\Psi(P_0)\), which is the quantity we wish to learn from the data. Once we have defined \(O\), \(\M\) and \(\Psi(P_0)\) we have formally defined the statistical estimation problem.

(4) The estimator \(\hat{\Psi}\) and estimate \(\hat{\Psi}(P_n)\)

Typically, we will focus on estimation in realistic, nonparametric models. To obtain a good approximation of the estimand, we need an estimator, an a priori-specified algorithm defined as a mapping from the set of possible empirical distributions, \(P_n\), which live in a non-parametric statistical model, \(\M_{NP}\) (\(P_n \in \M_{NP}\)), to the parameter space of the parameter of interest. That is, \(\hat{\Psi} : \M_{NP} \rightarrow \R^d\). The estimator is a function that takes as input the observed data, a realization of \(P_n\), and gives as output a value in the parameter space, which is the estimate, \(\hat{\Psi}(P_n)\).

Where the estimator may be seen as an operator that maps the observed data and corresponding empirical distribution to a value in the parameter space, the numerical output that produced such a function is the estimate. Thus, it is an element of the parameter space based on the empirical probability distribution of the observed data. If we plug in a realization of \(P_n\) (based on a sample size \(n\) of the random variable \(O\)), we get back an estimate \(\hat{\Psi}(P_n)\) of the true parameter value \(\Psi(P_0)\).

In order to quantify the uncertainty in our estimate of the target parameter (i.e., to construct statistical inference), an understanding of the sampling distribution of our estimator will be necessary. This brings us to Step 5.

(5) A measure of uncertainty for the estimate \(\hat{\Psi}(P_n)\)

Since the estimator \(\hat{\Psi}\) is a function of the empirical distribution \(P_n\), the estimator itself is a random variable with a sampling distribution. So, if we repeat the experiment of drawing \(n\) observations we would every time end up with a different realization of our estimate and our estimator has a sampling distribution.

A primary goal in the construction of estimators is to be able to derive their asymptotic sampling distributions through a theoretical analysis of a given estimator. In this regard, an important property of the estimators on which we focus is their asymptotic linearity, which states that the difference between the estimator and the target estimand (i.e., the truth) can be represented, asymptotically, as an average of i.i.d. random variables:

\[\begin{equation*} \hat{\Psi}(P_n) - \Psi(P_0) = \frac{1}{n} \sum_{i=1}^n IC(O_i; \nu) + o_p(n^{-1/2}), \end{equation*}\] where \(\nu\) represents possible nuisance parameters on which the influence curve (IC) depends. Based on the validity of the asymptotic approximation, one can then invoke the central limit theorem (CLT) to show

\[\begin{equation*} \sqrt{n} \left(\hat{\Psi}(P_n) - \Psi(P_0)\right) \sim N(0, \sigma^2_{IC}), \end{equation*}\] where \(\sigma^2_{IC}\) is the variance of \(IC(O_i; \nu)\). Given an estimate of \(\sigma^2_{IC}\), it is then possible to construct classic, asymptotically accurate Wald-type confidence intervals (CIs) and hypothesis tests. For example, a standard \((1 - \alpha)\) CI of the form

\[\begin{equation*} \Psi(P_n) \pm Z_{1 - \frac{\alpha}{2}} \hat{\sigma_{IC}} / \sqrt{n}, \end{equation*}\] can be constructed, where \(Z_{1 - \frac{\alpha}{2}}\) is the \((1 - \frac{\alpha}{2})^\text{th}\) quantile of the standard normal distribution. Often, we will be interested in constructing 95% confidence intervals, corresponding to mass \(\alpha = 0.05\) in either tail of the limit distribution; thus, we will typically take \(Z_{1 - \frac{\alpha}{2}} \approx 1.96\).

2.2 Summary of the Roadmap

Data collected across \(n\) i.i.d. units, \(O_1, \ldots, O_n\), can be viewed as a collection of random variables, \(O\), all arising from the same probability distribution \(\P_0\). This collection of data may be expressed \(O_1, \ldots, O_n \sim P_0\), where we leverage statistical knowledge available about the experiment that generated the data. to support the statement that the true data distribution \(P_0\) falls in a statistical model, \(\M\), which is itself a collection of candidate probability distributions reflecting the data-generating experiment. Often these sets — that is, the statistical model \(\M\) — must be very large, to appropriately reflect the fact that statistical knowledge is very limited. Hence, these realistic statistical models are often termed semi- or non-parametric, since they are too large to be indexed by a finite-dimensional set of parameters. Necessarily, our statistical query must begin with, “What are we trying to learn from the data?”, a question whose answer is captured by the statistical target parameter, \(\Psi\), which maps the true data-generating distribution \(P_0\) into the statistical estimand, \(\Psi(P_0)\). At this point the statistical estimation problem is formally defined, allowing for the use of statistical theory to guide the construction of optimal estimators.

2.3 Causal Target Parameters

In many cases, we are interested in problems that ask questions regarding the causal effect of an intervention on a future outcome of interest. These causal effects may be defined as summaries of the population of interest (e.g., the population mean of a particular outcome) under different conditions (e.g., treated versus untreated). For example, a causal effect could be defined as the difference in the means of a disease outcome between causal contrasts in which the population were to experience low pollution levels (for some pollutant) and the mean in the same population in the case that high pollution levels were experienced. There are different ways of operationalizing the theoretical experiments that generate the counterfactual data necessary for describing our causal contrasts of interest, including simply assuming that the counterfactual outcomes exist in theory for all treatment contrasts of interest (Neyman 1938; Rubin 2005; Imbens and Rubin 2015) or through considering interventions on directed acyclic graphs (DAGs) or nonparametric structural equation models (NPSEMs) (Pearl 1995, 2009), both of which encode the known or hypothesized set of relationships between variables in the system under study.

The Causal Model

We focus on the use of DAGs and NPSEMs for the description of causal parameters. Estimators of statistical parameters that correspond, under standard but untestable identifiability assumptions, to these causal parameters are introduced below. DAGs are a particularly useful tool for expressing what we know about the causal relations among variables in the system under study. Ignoring exogenous \(U\) terms (explained below), we assume the following ordering of the variables in the observed data \(O\). We demonstrate the construction of a DAG below using DAGitty (Textor, Hardt, and Knüppel 2011):

library(dagitty)
library(ggdag)
# make DAG by specifying dependence structure
dag <- dagitty(
  "dag {
    W -> A
    W -> Y
    A -> Y
    W -> A -> Y
  }"
)
exposures(dag) <- c("A")
outcomes(dag) <- c("Y")
tidy_dag <- tidy_dagitty(dag)
# visualize DAG
ggdag(tidy_dag) +
  theme_dag()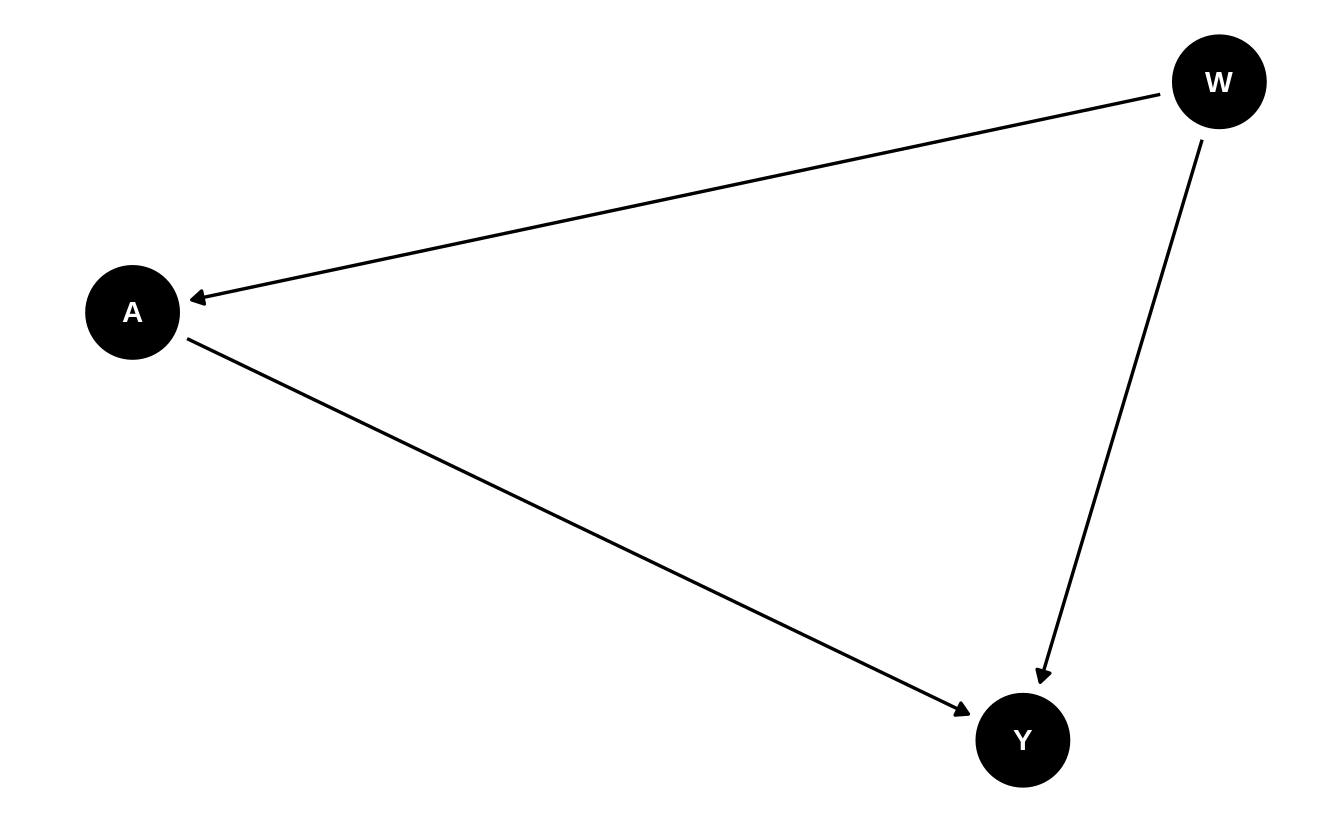

While DAGs like the above provide a convenient means by which to visualize causal relations between variables, the same causal relations among variables can be equivalently represented by an NPSEM: \[\begin{align*} W &= f_W(U_W) \\ A &= f_A(W, U_A) \\ Y &= f_Y(W, A, U_Y), \end{align*}\] where the \(f\)’s are unspecified (non-parametric) functions that generate the corresponding random variable as a function of the variable’s parents (i.e., nodes with arrows into the variable) in the DAG and the unobserved, exogenous error terms (i.e., the \(U\)’s). An NPSEM may be thought of as a representation of the algorithm that produces the data, \(O\), in the population of interest. Much of statistics and data science is devoted to discovering properties of this system of equations (e.g., estimation of the prediction function \(f_Y\)).

The first hypothetical experiment we will consider is assigning exposure to the entire population and observing the outcome, and then withholding exposure to the same population and observing the outcome. This corresponds to a comparison of the outcome distribution in the population under two interventions:

  1. \(A\) is set to \(1\) for all individuals, and
  2. \(A\) is set to \(0\) for all individuals.

These interventions imply two new sets of nonparametric structural equations For the case \(A = 1\), we have \[\begin{align*} W &= f_W(U_W) \\ A &= 1 \\ Y(1) &= f_Y(W, 1, U_Y), \end{align*}\] while, for the case \(A=0\), \[\begin{align*} W &= f_W(U_W) \\ A &= 0 \\ Y(0) &= f_Y(W, 0, U_Y). \end{align*}\]

In these equations, \(A\) is no longer a function of \(W\) because of the intervention on the system that set \(A\) deterministically to either of the values \(1\) or \(0\). The new symbols \(Y(1)\) and \(Y(0)\) indicate the outcome variable in the population of interest when it is generated by the respective NPSEMs above; these are often called counterfactuals. The difference between the means of the outcome under these two interventions defines a parameter that is often called the “average treatment effect” (ATE), denoted

\[\begin{equation} ATE = \E_X(Y(1) - Y(0)), \tag{2.1} \end{equation}\] where \(\E_X\) is the mean under the theoretical (unobserved) full data \(X = (W, Y(1), Y(0))\).

Note, we can define much more complicated interventions on NPSEM’s, such as interventions based upon rules (themselves based upon covariates), stochastic rules, etc. and each results in a different targeted parameter and entails different identifiability assumptions discussed below.

Identifiability

Because we can never observe both \(Y(0)\) (the counterfactual outcome when \(A=0\)) and \(Y(1)\) (similarly, the counterfactual outcome when \(A=1\)), we cannot estimate the quantity in Equation (2.1) directly. Thus, the primary task of causal inference methods in our context is to identify the assumptions necessary to express causal quantities of interest as functions of the data-generating distribution. We have to make assumptions under which this quantity may be estimated from the observed data \(O \sim P_0\) under the data-generating distribution \(P_0\). Fortunately, given the causal model specified in the NPSEM above, we can, with a handful of untestable assumptions, estimate the ATE from observational data. These assumptions may be summarized as follows.

  1. No unmeasured confounding: \(A \perp Y(a) \mid W\) for all \(a \in \mathcal{A}\), which states that the potential outcomes \((Y(a) : a \in \mathcal{A})\) arise independently from exposure status \(A\), conditional on the observed covariates \(W\). This is the analog of the randomization assumption in data arising from natural experiments, ensuring that the effect of \(A\) on \(Y\) can be disentangled from that of \(W\) on \(Y\), even though \(W\) affects both.
  2. No interference between units: the outcome for unit \(i\), \(Y_i\), cannot be affected by the exposure of unit \(j\), \(A_j\), for all \(i \neq j\).
  3. Consistency of the treatment mechanism is also required, i.e., the outcome for unit \(i\) is \(Y_i(a)\) whenever \(A_i = a\), an assumption also known as “no other versions of treatment”.
  4. Positivity or overlap: All observed units, across strata defined by \(W\), must have a bounded (non-deterministic) probability of receiving treatment — that is, \(0 < \P(A = a \mid W) < 1\) for all \(a\) and \(W\)).

Given these assumptions, the ATE may be re-written as a function of \(P_0\), specifically

\[\begin{equation} ATE = \E_0(Y(1) - Y(0)) = \E_0 \left(\E_0[Y \mid A = 1, W] - \E_0[Y \mid A = 0, W]\right). \tag{2.2} \end{equation}\] In words, the ATE is the difference in the predicted outcome values for each subject, under the contrast of treatment conditions (\(A = 0\) versus \(A = 1\)), in the population, averaged over all observations. Thus, a parameter of a theoretical “full” data distribution can be represented as an estimand of the observed data distribution. Significantly, there is nothing about the representation in Equation (2.2) that requires parameteric assumptions; thus, the regressions on the right hand side may be estimated. With different parameters, there will be potentially different identifiability assumptions and the resulting estimands can be functions of different components of \(P_0\). We discuss several more complex estimands in later sections.

2.4 Exercises

  1. Introduction

    1. Why did you enroll in this course?
    2. Have you had educational and/or work experiences related to the topics covered in this course, including causal inference, data analysis, statistics, machine learning?

  2. What is the objective of the roadmap?

  3. Specifying a statistical estimation problem consists of what three steps?

  4. Provide a definition and an example for each of the following:

    1. Statistical model
    2. Target estimand
    3. Estimator

  5. Provide examples of data under the following scenarios:

    1. The observations are not independent, but are identically distributed.
    2. The observations are neither independent nor identically distributed.

  6. Traditional data analysis concerns

    1. Common data science practice encourages users to “check” models after they have been fit to the data so that if one of the checks fail, then a new model can be fit to the data. Why can this approach be problematic?
    2. Common data science practice lets the type of data at hand dictate the scientific question of interest and the statistical model. Why is this problematic?

Exercise Solutions

After all exercises are submitted, the solutions will be made available here: Roadmap Exercise Solutions.