4 Cross-validation

Ivana Malenica

Based on the origami R package by Jeremy Coyle, Nima Hejazi, Ivana Malenica and Rachael Phillips.

Updated: 2021-08-18

Learning Objectives

By the end of this chapter you will be able to:

Reliably assess the performance of a machine learning algorithm, or compare the performance of several algorithms by applying cross-validation schemes using the origami R package.

4.1 Introduction

In this chapter, we start elaborating on the estimation step outlined in the introductory chapter, which discussed the Roadmap for Targeted Learning. In order to generate an initial estimate of our target parameter — which is the focus of the following chapter on Super Learning, we first need to translate, and incorporate, our knowledge about the data generating process into the estimation procedure, and decide how to evaluate our estimation performance.

The performance, or error, of any algorithm used in the estimation procedure directly relates to its generalizability on the independent data. The proper assessment of the performance of proposed algorithms is extremely important; it guides the choice of the final learning method, and it gives us a quantitative assessment of how good the chosen algorithm is doing. In order to assess the performance of an algorithm, we introduce the concept of a loss function, which helps us define the risk, also referred to as the expected prediction error.

Constructing a library that is consistent with the data-generating distribution

Our goal, as further specified in the next chapter, will be to estimate the true risk of the proposed statistical learning method. Our goal(s) consist of:

Estimating the performance of different algorithms in order to choose the best one.
Having chosen a winner, estimate the true risk of the proposed statistical learning method.

In the following, we propose a method to do so using the observed data and cross-validation procedure using the origami package (Coyle and Hejazi 2018).

4.2 Background

Ideally, in a data-rich scenario, we would split our dataset into three parts:

training set,
validation set,
test set.

The training set is used to fit algorithm(s) of interest; we evaluate the performance of the fit(s) on a validation set, which can be used to estimate prediction error (e.g., for tuning and model selection). The final error of the chosen algorithm(s) is obtained by using the test set, which is kept separately, and doesn’t see the data before the final evaluation. One might wonder, with training data readily available, why not use the training error to evaluate the proposed algorithm’s performance? Unfortunately, the training error is not a good estimate of the true risk; it consistently decreases with model complexity, resulting in a possible overfit to the training data and low generalizability.

Since data are often scarce, separating it into training, validation and test set is usually not possible. In the absence of a large data set and a designated test set, we must resort to methods that estimate the true risk by efficient sample re-use. Re-sampling methods, in great generality, involve repeatedly sampling from the training set and fitting proposed algorithms on the new samples. While often computationally intensive, re-sampling methods are particularly useful for model selection and estimation of the true risk. In addition, they might provide more insight on variability and robustness of the algorithm fit then fitting an algorithm only once on all the training data.

4.2.1 What is cross-validation?

In this chapter, we focus on cross-validation — an essential tool for evaluating how any given algorithm extends from a sample to the target population from which the sample is derived. It has seen widespread application in all facets of statistics, perhaps most notably statistical machine learning. The cross-validation procedure can be used for model selection, as well as for estimation of the true risk associated with any statistical learning method in order to evaluate its performance. It particular, cross-validation directly estimates the true risk when the estimate is applied to an independent sample from the joint distribution of the predictors and outcome. When used for model selection, cross-validation has powerful optimality properties. The asymptotic optimality results state that the cross-validated selector performs (in terms of risk) asymptotically as well as an optimal oracle selector based on the true, unknown data generating distribution. For further details on the theoretical results, we suggest van der Laan and Dudoit (2003), van der Laan, Dudoit, and Keles (2004), Dudoit and van der Laan (2005) and Van der Vaart, Dudoit, and Laan (2006).

In great generality, cross-validation works by partitioning a sample into complementary subsets, applying a particular algorithm(s) on a subset (the training set), and evaluating the method of choice on the complementary subset (the validation/test set). This procedure is repeated across multiple partitions of the data. A variety of different partitioning schemes exist, depending on the problem of interest, data size, prevalence of the outcome, and dependence structure. The origami package provides a suite of tools that generalize the application of cross-validation to arbitrary data analytic procedures. In the the following, we describe different types of cross-validation schemes readily available in origami, introduce the general structure of the origami package, and show their use in applied settings.

4.3 Roadmap: How does it all fit together?

Similarly to how we defined the Roadmap for Targeted Learning, we can define the Estimation Roadmap to guide the estimation process. In particular, we have developed a unified loss-based cross-validation methodology for estimator construction, selection, and performance assessment in a series of articles (e.g., see van der Laan and Dudoit (2003), van der Laan, Dudoit, and Keles (2004), Dudoit and van der Laan (2005), Van der Vaart, Dudoit, and Laan (2006), and van der Laan, Polley, and Hubbard (2007)) that follow three main steps:

The loss funtion: Define the target parameter as the minimizer of the expected loss (risk) for a full data loss function chosen to represent the desired performance measure. Map the full data loss function into an observed data loss function, having the same expected value and leading to an efficient estimator of risk.
The algorithms: Construct a finite collection of candidate estimators for the parameter of interest.
The cross-validation scheme: Apply appropriate cross-validation to select an optimal estimator among the candidates, and assess the overall performance of the resulting estimator.

Step 1 of the Estimation Roadmap allows us to unify a broad range of problems that are traditionally treated separately in the statistical literature, including density estimation, prediction of polychotomous and continuous outcomes. For example, if we are interested in estimating the full joint conditional density, we could use the negative log-likelihood loss. If instead we are interested in the conditional mean with continuous outcome, one could use the squared error loss; had the outcome been binary, one could resort to the indicator (0-1) loss. The unified loss-based framework also reconciles censored and full data estimation methods, by generalizing any loss based learning for full data into loss based learning for general censored data.

4.4 Example: cross-validation and prediction

Now that we introduced the Estimation Roadmap, we can define our objective with more mathematical notation, using prediction as an example. Let the observed data be defined as \(X = (W,Y)\), where a unit specific data can be written as \(X_i = (W_i,Y_i)\), for \(i = 1, \ldots, n\). For each of the \(n\) samples, we denote \(Y_i\) as the outcome of interest (polychotomous or continuous), and \(W_i\) as a \(p\)-dimensional set of covariates. Let \(\psi_0(W)\) denote the target parameter of interest we want to estimate; for this example, we are interested in estimating the conditional expectation of the outcome given the covariates, \(\psi_0(W) = E(Y \mid W)\). Following the Estimation Roadmap, we chose the appropriate loss function, \(L\), such that \(\psi_0(W) = \text{argmin}_{\psi} E[L(X,\psi(W))]\). But how do we know how each \(\psi\) is doing? In order to pick the optimal estimator among the candidates, and assess the overall performance of the resulting estimator, we use cross-validation — dividing the available data into the training set and validation set. Observations in the training set are used to fit (or train) the estimator, while the validation set is used to assess the risk of (or validate) it.

To derive a general representation for cross-validation, we define a split vector, \(B_n = (B_n(i): i = 1, \ldots, n) \in \{0,1\}^n\). Note that split vector is independent of the empirical distribution, \(P_n\). A realization of \(B_n\) defines a random split of the data into a training and validation set such that if

\[B_n(i) = 0, \ \ \text{i sample is in the training set}\] \[B_n(i) = 1, \ \ \text{i sample is in the validation set.}\] We can further define \(P_{n,B_n}^0\) and \(P_{n,B_n}^1\) as the empirical distributions of the training and validation sets, respectively. Then \(n_0 = \sum_i (1-B_n(i))\) and \(n_1 = \sum_i B_n(i)\) denote the number of samples in each set. The particular distribution of the split vector \(B_n\) defines the type of cross-validation scheme, tailored to the problem and data set in hand.

4.5 Cross-validation schemes in `origami`

As we specified earlier, the particular distribution of the split vector \(B_n\) defines the type of the cross-validation method. In the following, we describe different types of cross-validation schemes available in origami package, and show their use in the sequel.

WASH Benefits study example

In order to illustrate different cross-validation schemes, we will be using the WASH data. Detailed information on the WASH Benefits example dataset can be found in Chapter 3. In particular, we are interested in predicting weight-for-height z-score whz using the available covariate data. For this illustration, we will start by treating the data as independent and identically distributed (i.i.d.) random draws. To see what each cross-validation scheme is doing, we will subset the data to only \(n=30\). Note that each row represents an i.i.d. sample, indexed by the row number.

library(data.table)
library(origami)
library(knitr)
library(kableExtra)

# load data set and take a peek
washb_data <- fread(
  paste0(
    "https://raw.githubusercontent.com/tlverse/tlverse-data/master/",
    "wash-benefits/washb_data.csv"
  ),
  stringsAsFactors = TRUE
)

whz	tr	fracode	month	aged	sex	momage	momedu	momheight	hfiacat	Nlt18	Ncomp	watmin	elec	walls	roof	asset_wardrobe	asset_table	asset_chair	asset_khat	asset_chouki	asset_tv	asset_bike	asset_mobile
0.00	Control	N05265	9	268	male	30	Primary (1-5y)	146.40	Food Secure	3	11	0	1	1	1	0	1	1	1	0	1	0	1
-1.16	Control	N05265	9	286	male	25	Primary (1-5y)	148.75	Moderately Food Insecure	2	4	0	1	1	1	0	1	0	1	1	0	0	1
-1.05	Control	N08002	9	264	male	25	Primary (1-5y)	152.15	Food Secure	1	10	0	0	1	1	0	0	1	0	1	0	0	1
-1.26	Control	N08002	9	252	female	28	Primary (1-5y)	140.25	Food Secure	3	5	0	1	1	1	1	1	1	1	0	0	1	1
-0.59	Control	N06531	9	336	female	19	Secondary (>5y)	150.95	Food Secure	2	7	0	1	1	1	1	1	1	1	1	0	0	1
-0.51	Control	N06531	9	304	male	20	Secondary (>5y)	154.20	Severely Food Insecure	0	3	1	1	1	1	0	0	0	0	1	0	0	1

Above is a look at the first 30 of the data.

4.5.1 Cross-validation for i.i.d. data

4.5.1.1 Re-substitution

The re-substitution method is the simplest strategy for estimating the risk associated with fitting a proposed algorithm on a set of observations. Here, all observed data is used for both training and validation set.

We illustrate the usage of the re-substitution method with origami package below; we will use the function folds_resubstitution(n). In order to setup folds_resubstitution(n), we just need the total number of samples we want to allocate to training and validation sets; remember that each row of data is a unique i.i.d. sample. Notice the structure of the origami output:

v: the cross-validation fold
training_set: the indexes of the samples in the training set
validation_set: the indexes of the samples in the training set.

This structure of the origami output (aka, fold(s)) will persist for each of the cross-validation schemes we present in this chapter. Below, we show the fold generated by the re-substitution method:

folds_resubstitution(nrow(washb_data))
#> [[1]]
#> $v
#> [1] 1
#> 
#> $training_set
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> [26] 26 27 28 29 30
#> 
#> $validation_set
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> [26] 26 27 28 29 30
#> 
#> attr(,"class")
#> [1] "fold"

4.5.1.2 Holdout method

The holdout method, or the validation set approach, consists of randomly dividing the available data into the training set and validation set (holdout set). The model is then fitted on the training set, and further evaluated on the observations in the validation set. Typically, the data is split into \(60/40\), \(70/30\), \(80/20\) or \(90/10\) splits.

The holdout method is intuitive, conceptually easy, and computationally not too demanding. However, if we repeat the process of randomly splitting the data into the training and validation set, we might get a very different cross-validated emprical risk. In particular, the emprical mean of the loss over the validation sets might be highly variable, depending on which samples were included in the training/validation split. Overall, the cross-validated emprical risk for the holdout method is more variabiable, since in includes variability of the random split as well - which is not what we want. For classification problems, there is a possibility of an uneven distribution of different classes in the training and validation set unless data is stratified. Finally, note that we are not using all of the data to train and evaluate the performance of the proposed algorithm, which might result in bias.

4.5.1.3 Leave-one-out

The leave-one-out cross-validation scheme is closely related to the holdout method. In particular, it also involves splitting the data into the training and validation set; however, instead of partitioning the observed data into sets of similar size, a single observation is used as a validation set. With that, majority of the units are employed for training (fitting) the proposed algorithm. Since only one unit (for example \(x_1 = (w_1, y_1)\)) is not used in the fitting process, leave-one-out cross-validation results in a possibly less biased estimate of the true risk; typically, leave-one-out approach will not overestimate the risk as much as the holdout method. On the other hand, since the estimate of risk is based on a single sample, it is typically a highly variable estimate.

We can repeat the process of spiting the data into training and validation set until all samples are part of the validation set at some point. For example, next iteration of the cross-validation might have \(x_2 = (w_2,y_2)\) as the validation set and all the rest of \(n-1\) samples as the training set. Repeating this approach \(n\) times results in, for example, \(n\) squared errors \(MSE_1, MSE_2, \ldots, MSE_n\). The estimate of the true risk is the average over the \(n\) squared errors. While the leave-one-out cross-validation results in a less biased (albeit, more variable) estimate of risk than the holdout method, it could be expensive to implement if \(n\) is large.

We illustrate the usage of the leave-one-out cross-validation with origami package below; we will use the function folds_loo(n). In order to setup folds_loo(n), similarly to the re-substitution method, we just need the total number of samples we want to cross-validate. We show the first two folds generated by the leave-one-out cross-validation below.

folds <- folds_loo(nrow(washb_data))
folds[[1]]
#> $v
#> [1] 1
#> 
#> $training_set
#>  [1]  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
#> [26] 27 28 29 30
#> 
#> $validation_set
#> [1] 1
#> 
#> attr(,"class")
#> [1] "fold"
folds[[2]]
#> $v
#> [1] 2
#> 
#> $training_set
#>  [1]  1  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
#> [26] 27 28 29 30
#> 
#> $validation_set
#> [1] 2
#> 
#> attr(,"class")
#> [1] "fold"

4.5.1.4 V-fold

An alternative to leave-one-out is V-fold cross-validation. This cross-validation scheme randomly divides the data into \(v\) sets (folds) of equal size; for each fold, the number of samples in the validation set are the same. For V-fold cross-validation, one of the folds is treated as a validation set, whereas the proposed algorithm is fit on the remaining \(v-1\) folds in the training set. The loss, for example MSE, is computed on the samples in the validation set. With the proposed algorithm trained and its performance evaluated on the first fold, we repeat this process \(v\) times; each time, a different group of samples is treated as a validation set. Note that with V-fold cross-validation we effectively use all of the data to train and evaluate the proposed algorithm without overfitting to the training data. In the end, the V-fold cross-validation results in \(v\) estimates of validation error. The final V-fold CV estimate is computed as an average over all the validation losses.

For a dataset with \(n\) samples, V-fold cross-validation with \(v=n\) is just leave-one-out; similarly, if we set \(n=1\), we can get the holdout method’s estimate of algorithm’s performance. Despite the obvious computational advantages, V-fold cross-validation often gives more accurate estimates of the true risk. The reason for this comes from the bias-variance trade-off that comes from employing both methods; while leave-one-out might be less biased, it has higher variance. This difference becomes more obvious as \(v<<n\) (but not too small, as then we increase bias). With V-fold cross-validation, we end up averaging output from \(v\) fits that are typically less correlated than the outputs from leave-one-out fits. Since the mean of many highly correlated quantities has higher variance, leave-one-out estimate of the risk will have higher variance than the estimate based on V-fold cross-validation.

Let’s see V-fold cross-validation with origami in action! In the next chapter we will study the Super Learner — an actual algorithm that we fit and evaluate its performance. The Super Learner relies on V-fold cross-validation as default cross-validation scheme. In order to set up V-fold CV, we need to call function folds_vfold(n, V). Arguments for folds_vfold(n, V) require the total number of samples to be cross-validated, and the number of folds we want to get.

At \(V=2\), we get 2 folds with \(n/2\) number of samples in both training and validation set.

folds <- folds_vfold(nrow(washb_data), V = 2)
folds[[1]]
#> $v
#> [1] 1
#> 
#> $training_set
#>  [1]  2  3  4  6  7  8 11 12 14 15 19 22 23 24 28
#> 
#> $validation_set
#>  [1]  1  5  9 10 13 16 17 18 20 21 25 26 27 29 30
#> 
#> attr(,"class")
#> [1] "fold"
folds[[2]]
#> $v
#> [1] 2
#> 
#> $training_set
#>  [1]  1  5  9 10 13 16 17 18 20 21 25 26 27 29 30
#> 
#> $validation_set
#>  [1]  2  3  4  6  7  8 11 12 14 15 19 22 23 24 28
#> 
#> attr(,"class")
#> [1] "fold"

4.5.1.5 Monte Carlo

With Monte Carlo cross-validation, we randomly select some fraction of the data (without replacement) to form the training set; we assign the rest of the samples to the validation set. With that, the data is repeatedly and randomly divided into two sets, a training set of \(n_0 = n \cdot (1-p)\) observations and a validation set of \(n_1 = n \cdot p\) observations. This process is then repeated multiple times, generating (at random) new training and validation partitions each time.

Since the partitions are independent across folds, the same sample can appear in the validation set multiple times — note that this is a stark difference between Monte Carlo and V-fold cross-validation. For a given \(p\), Monte Carlo cross-validation would be optimal if done infinite times, but this is not computationally feasible. With Monte Carlo cross-validation, one is able to explore many more available partitions than with V-fold cross-validation — resulting in a possibly less variable estimate of the risk, at a cost of an increase in bias. By having many overlapping splits, we often also need more splits (and thus more computational time) to achieve V-fold performance with only \(V\) splits.

We illustrate the usage of the Monte Carlo cross-validation with origami package below using the function folds_montecarlo(n, V, pvalidation). In order to setup folds_montecarlo(n, V, pvalidation), we need

the total number of samples we want to cross-validate (n);
the number of folds (V);
the proportion of observations to be placed in the validation set (pvalidation).

At V=2 and pvalidation=0.2, we obtain 2 folds with approximately \(6\) samples in validation set per fold.

folds <- folds_montecarlo(nrow(washb_data), V = 2, pvalidation = 0.2)
folds[[1]]
#> $v
#> [1] 1
#> 
#> $training_set
#>  [1] 19 27 16 29 23 12  1  3 18 11  5  7  8  6  9 22 10 25 20 28 15  2 24 26
#> 
#> $validation_set
#> [1]  4 13 14 17 21 30
#> 
#> attr(,"class")
#> [1] "fold"
folds[[2]]
#> $v
#> [1] 2
#> 
#> $training_set
#>  [1] 19 15 28 25 29 11 20 17 14  4  9 12 30  8 27 18 16 10 13  6 24  3 26  1
#> 
#> $validation_set
#> [1]  2  5  7 21 22 23
#> 
#> attr(,"class")
#> [1] "fold"

4.5.1.6 Bootstrap

The bootstrap cross-validation also consists of randomly selecting samples, with replacement, for the training set. The rest of the samples not picked for the training set are allocated to the validation set. This process is then repeated multiple times, generating (at random) new training and validation partitions each time. In contract to the Monte Carlo cross-validation, the total number of samples in a training and validation size across folds is not constant. We also sample with replacement, hence the same samples can be in multiple training sets. The proportion of observations in the validation sets is a random variable, with expectation \(\sim 0.368\).

We illustrate the usage of the bootstrap cross-validation with origami package below using the function folds_bootstrap(n, V). In order to setup folds_bootstrap(n, V), we need

the total number of samples we want to cross-validate (n); and
the number of folds (V).

At \(V=2\), we obtain \(2\) folds with different number of samples in the validation set across folds.

folds <- folds_bootstrap(n = nrow(washb_data), V = 2)
folds[[1]]
#> $v
#> [1] 1
#> 
#> $training_set
#>  [1]  2  5 30  1 29 16 10 11  8 25 28  2 11  2 16 28 15 28  1 27  9 19 20 30 18
#> [26] 11 13  2 18 12
#> 
#> $validation_set
#>  [1]  3  4  6  7 14 17 21 22 23 24 26
#> 
#> attr(,"class")
#> [1] "fold"
folds[[2]]
#> $v
#> [1] 2
#> 
#> $training_set
#>  [1] 12 16 10 29 22 15 27  9 27 16 12 28 10 28 26  1 14  6 23 14 21 16  5 20  8
#> [26] 23 25  8 27  5
#> 
#> $validation_set
#>  [1]  2  3  4  7 11 13 17 18 19 24 30
#> 
#> attr(,"class")
#> [1] "fold"

4.5.2 Cross-validation for dependent data

The origami package also supports numerous cross-validation schemes for time-series data, for both single and multiple time-series with arbitrary time and network dependence.

AirPassenger Example

In order to illustrate different cross-validation schemes for time-series, we will be using the AirPassenger data; this is a widely used, freely available dataset. The AirPassenger dataset in R provides monthly totals of international airline passengers from 1949 to 1960. This dataset is already of a time series class therefore no further class or date manipulation is required.

Constructing a library that is consistent with the data-generating distribution Goal: we want to forecast the number of airline passengers at some future time (i.e., horizon) \(h\) using the historical data from 1949 to 1960.

library(ggfortify)

data(AirPassengers)
AP <- AirPassengers

autoplot(AP) +
  labs(
    x = "Date",
    y = "Passenger numbers (1000's)",
    title = "Air Passengers from 1949 to 1961"
  )

t <- length(AP)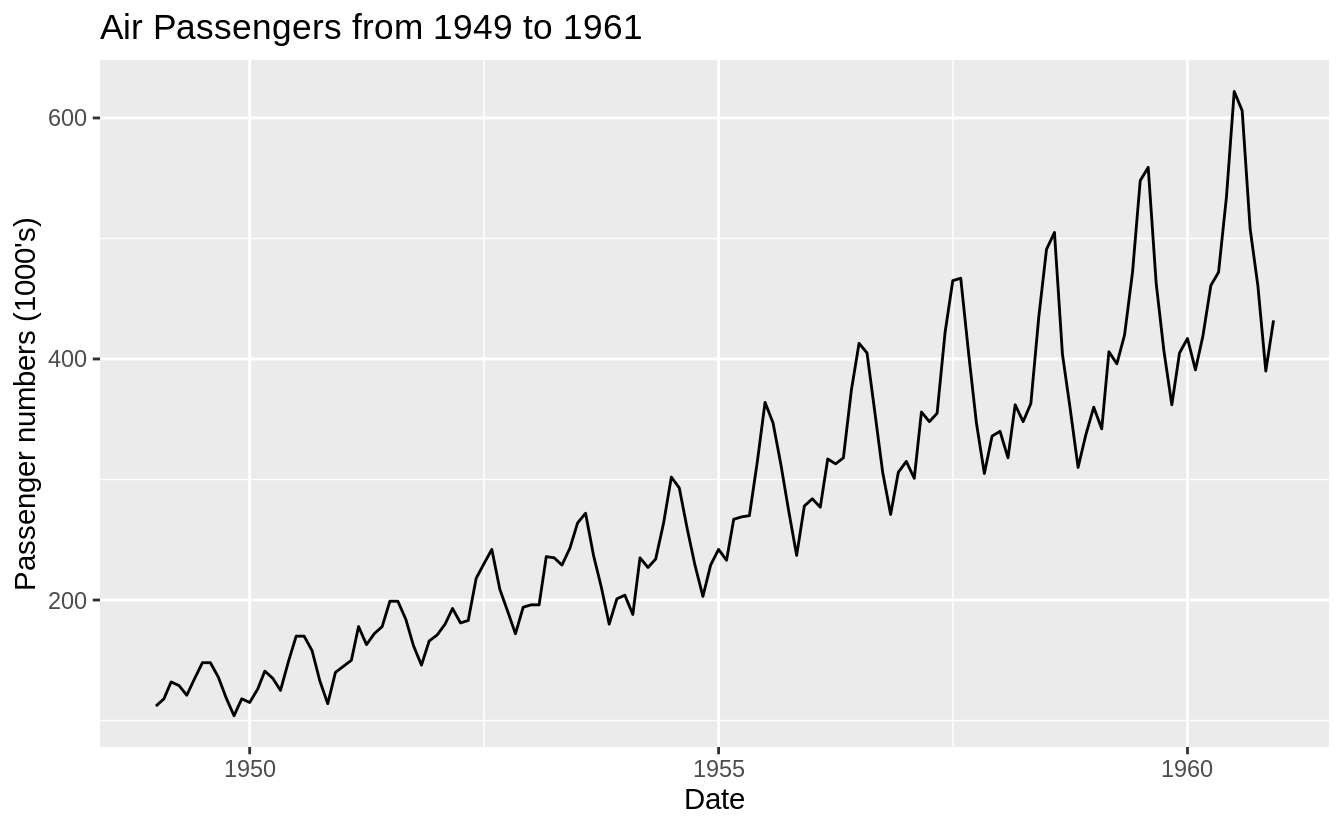

4.5.2.1 Rolling origin

Rolling origin cross-validation scheme lends itself to “online” algorithms, where large streams of data have to be fit continually, and the final fit is constantly updated with more data acquired. In general, the rolling origin scheme defines an initial training set, and with each iteration the size of the training set grows by \(m\) observations until we reach time \(t\) for a particular fold. The time points included in the training set are always behind the validation set time points; in addition, there might be a gap between training and validation times of size \(h\).

To further illustrate rolling origin cross-validation, we show below an example with 3 folds. Here, the first window size is 15 time points, on which we first train the proposed algorithm. We then evaluate its performance on 10 time points, with a gap of size 5 between the training and validation time points. For the following fold, we train the algorithm on a longer stream of data, 25 time points, including the original 15 we started with. We then evaluate its performance on 10 time points in the future.

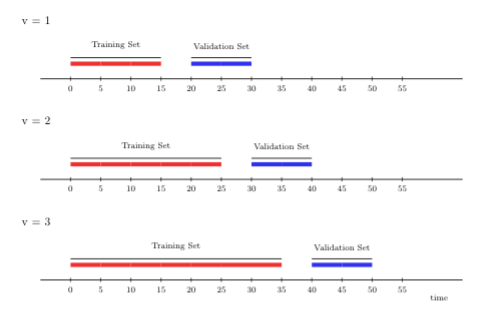
FIGURE 4.1: Rolling origin CV

We illustrate the usage of the rolling origin cross-validation with origami package below using the function folds_rolling_origin(n, first_window, validation_size, gap, batch). In order to setup folds_rolling_origin(n, first_window, validation_size, gap, batch), we need

the total number of time points we want to cross-validate (n);
the size of the first training set (first_window);
the size of the validation set (validation_size);
the gap between training and validation set (gap);
the size of the update on the training set per each iteration of CV (batch).

Our time-series has \(t=144\) time points. Setting the first_window to \(50\), validation_size to 10, gap to 5 and batch to 20, we get 4 time-series folds; we show the first two below.

folds <- folds_rolling_origin(
  t,
  first_window = 50, validation_size = 10, gap = 5, batch = 20
)
folds[[1]]
#> $v
#> [1] 1
#> 
#> $training_set
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
#> 
#> $validation_set
#>  [1] 56 57 58 59 60 61 62 63 64 65
#> 
#> attr(,"class")
#> [1] "fold"
folds[[2]]
#> $v
#> [1] 2
#> 
#> $training_set
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
#> [51] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70
#> 
#> $validation_set
#>  [1] 76 77 78 79 80 81 82 83 84 85
#> 
#> attr(,"class")
#> [1] "fold"

4.5.2.2 Rolling window

Instead of adding more time points to the training set per each iteration, the rolling window cross-validation scheme “rolls” the training sample forward by \(m\) time units. The rolling window scheme might be considered in parametric settings when one wishes to guard against moment or parameter drift that is difficult to model explicitly; it is also more efficient for computationally demanding settings such as streaming data, in which large amounts of training data cannot be stored. In contrast to rolling origin CV, the training sample for each iteration of the rolling window scheme is always the same.

To illustrate the rolling window cross-validation with 3 time-series folds below. The first window size is 15 time points, on which we first train the proposed algorithm. As in the previous illustration, we evaluate its performance on 10 time points, with a gap of size 5 between the training and validation time points. However, for the next fold, we train the algorithm on time points further away from the origin (here, 10 time points). Note that the size of the training set in the new fold is the same as in the first fold (15 time points). This setup keeps the training sets comparable over time (and fold) as compared to the rolling origin CV. We then evaluate the performance of the proposed algorithm on 10 time points in the future.

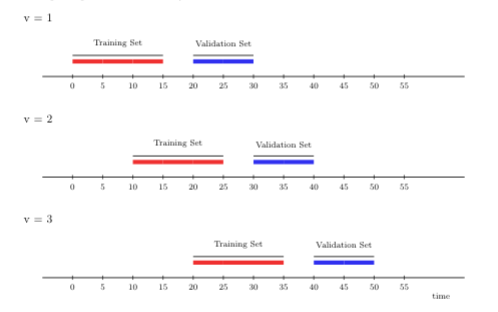
FIGURE 4.2: Rolling window CV

We illustrate the usage of the rolling window cross-validation with origami package below using the function folds_rolling_window(n, window_size, validation_size, gap, batch). In order to setup folds_rolling_window(n, window_size, validation_size, gap, batch), we need:

the total number of time points we want to cross-validate (n);
the size of the training sets (window_size);
the size of the validation set (validation_size);
the gap between training and validation set (gap); and
the size of the update on the training set per each iteration of CV (batch).

Setting the window_size to \(50\), validation_size to 10, gap to 5 and batch to 20, we also get 4 time-series folds; we show the first two below.

folds <- folds_rolling_window(
  t,
  window_size = 50, validation_size = 10, gap = 5, batch = 20
)
folds[[1]]
#> $v
#> [1] 1
#> 
#> $training_set
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
#> 
#> $validation_set
#>  [1] 56 57 58 59 60 61 62 63 64 65
#> 
#> attr(,"class")
#> [1] "fold"
folds[[2]]
#> $v
#> [1] 2
#> 
#> $training_set
#>  [1] 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
#> [26] 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70
#> 
#> $validation_set
#>  [1] 76 77 78 79 80 81 82 83 84 85
#> 
#> attr(,"class")
#> [1] "fold"

4.5.2.3 Rolling origin with V-fold

A variant of rolling origin scheme which accounts for sample dependence is the rolling-origin-\(V\)-fold cross-validation. In contrast to the canonical rolling origin CV, samples in the training and validation set are not the same, as the variant encompasses \(V\)-fold CV in addition to the time-series setup. The predictions are evaluated on the future times of time-series units not seen during the training step, allowing for dependence in both samples and time. One can use the rolling-origin-\(v\)-fold cross-validation with origami package using the function folds_vfold_rolling_origin_pooled(n, t, id, time, V, first_window, validation_size, gap, batch). In the figure below, we show \(V=2\) \(V\)-folds, and 2 time-series CV folds.

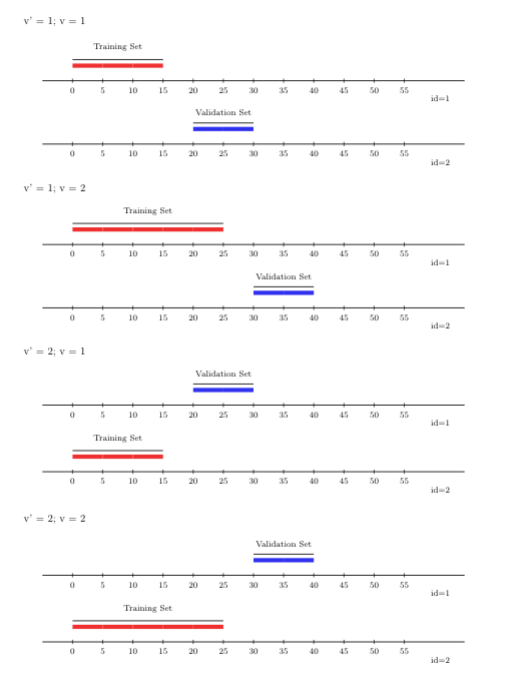
FIGURE 4.3: Rolling origin V-fold CV

4.5.2.4 Rolling window with V-fold

Analogous to the previous section, we can extend rolling window CV to support multiple time-series with arbitrary sample dependence. One can use the rolling-window-\(V\)-fold cross-validation with origami package using the function folds_vfold_rolling_window_pooled(n, t, id, time, V, window_size, validation_size, gap, batch). In the figure below, we show \(V=2\) \(V\)-folds, and 2 time-series CV folds.

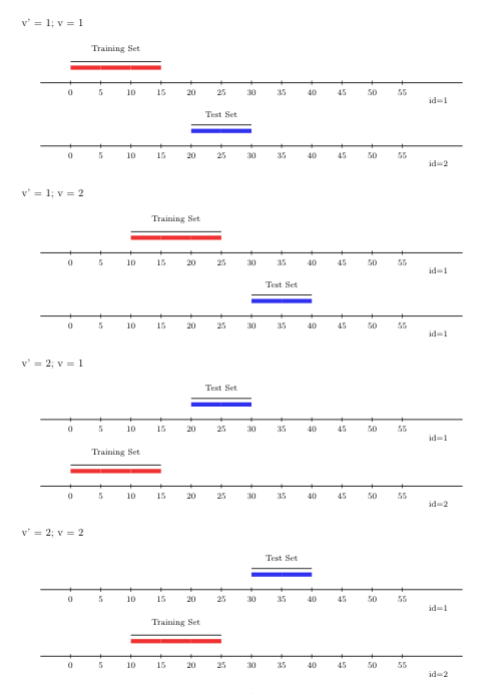
FIGURE 4.4: Rolling window V-fold CV

4.6 General workflow of `origami`

Before we dive into more details, let’s take a moment to review some of the basic functionality in origami R package. The main function in the origami is cross_validate. To start off, the user must define the fold structure and a function that operates on each fold. Once these are passed to cross_validate, cross_validate will apply the same specified function to each fold, and combine the fold-specific results in a meaningful way. We will see this in action in later sections; for now, we provide specific details on each each step of this process below.

(1) Define folds

The folds object passed to cross_validate is a list of folds; such lists can be generated using the make_folds function. Each fold consists of a list with a training index vector, a validation index vector, and a fold_index (its order in the list of folds). This function supports a variety of cross-validation schemes we describe in the following section. The make_folds can balance across levels of a variable (strata_ids), and it can also keep all observations from the same independent unit together (cluster).

(2) Define fold function

The cv_fun argument to cross_validate is a function that will perform some operation on each fold. The first argument to this function must be fold, which will receive an individual fold object to operate on. Additional arguments can be passed to cv_fun using the ... argument to cross_validate. Within this function, the convenience functions training, validation and fold_index can return the various components of a fold object. If training or validation is passed an object, it will index it in a sensible way. For instance, if it is a vector, it will index the vector directly; if it is a data.frame or matrix, it will index rows. This allows the user to easily partition data into training and validation sets. The fold function must return a named list of results containing whatever fold-specific outputs are generated.

(3) Apply `cross_validate`

After defining folds, cross_validate can be used to map the cv_fun across the folds using future_lapply. This means that it can be easily parallelized by specifying a parallelization scheme (i.e., a plan from the future parallelization framework for R (Bengtsson 2020)). The application of cross_validate generates a list of results. As described above, each call to cv_fun itself returns a list of results, with different elements for each type of result we care about. The main loop generates a list of these individual lists of results (a sort of “meta-list”). This “meta-list” is then inverted such that there is one element per result type (this too is a list of the results for each fold). By default, combine_results is used to combine these results type lists in a sensible manner. How results are combined is determined automatically by examining the data types of the results from the first fold. This can be modified by specifying a list of arguments to .combine_control.

4.7 Cross-validation in action

Let’s see origami in action! In the following chapter we will learn how to use cross-validation with the Super Learner, and how we can utilize the power of cross-validation to build optimal ensembles of algorithms, not just its use on a single statistical learning method.

4.7.1 Cross-validation with linear regression

First, we will load the relevant R packages, set a seed, and load the full WASH data once again. In order to illustrate cross-validation with origami and linear regression, we will focus on predicting the weight-for-height Z-score whz using all of the available covariate data. As stated previously, we will assume the data is independent and identically distributed, ignoring the cluster structure imposed by the clinical trial design. For the sake of illustration, we will work with a subset of data, and remove all samples with missing data from the dataset; we will learn in the next chapter how to deal with missingness.

library(stringr)
library(dplyr)
library(tidyr)

# load data set and take a peek
washb_data <- fread(
  paste0(
    "https://raw.githubusercontent.com/tlverse/tlverse-data/master/",
    "wash-benefits/washb_data.csv"
  ),
  stringsAsFactors = TRUE
)

# Remove missing data, then pick just the first 500 rows
washb_data <- washb_data %>%
  drop_na() %>%
  slice(1:500)

outcome <- "whz"
covars <- colnames(washb_data)[-which(names(washb_data) == outcome)]

Here’s a look at the data:

whz	tr	fracode	month	aged	sex	momage	momedu	momheight	hfiacat	Nlt18	Ncomp	watmin	elec	walls	roof	asset_wardrobe	asset_table	asset_chair	asset_khat	asset_chouki	asset_tv	asset_bike	asset_mobile
0.00	Control	N05265	9	268	male	30	Primary (1-5y)	146.40	Food Secure	3	11	0	1	1	1	0	1	1	1	0	1	0	1
-1.16	Control	N05265	9	286	male	25	Primary (1-5y)	148.75	Moderately Food Insecure	2	4	0	1	1	1	0	1	0	1	1	0	0	1
-1.05	Control	N08002	9	264	male	25	Primary (1-5y)	152.15	Food Secure	1	10	0	0	1	1	0	0	1	0	1	0	0	1
-1.26	Control	N08002	9	252	female	28	Primary (1-5y)	140.25	Food Secure	3	5	0	1	1	1	1	1	1	1	0	0	1	1
-0.59	Control	N06531	9	336	female	19	Secondary (>5y)	150.95	Food Secure	2	7	0	1	1	1	1	1	1	1	1	0	0	1
-0.51	Control	N06531	9	304	male	20	Secondary (>5y)	154.20	Severely Food Insecure	0	3	1	1	1	1	0	0	0	0	1	0	0	1

We can see the covariates used in the prediction:

outcome
#> [1] "whz"
covars
#>  [1] "tr"             "fracode"        "month"          "aged"          
#>  [5] "sex"            "momage"         "momedu"         "momheight"     
#>  [9] "hfiacat"        "Nlt18"          "Ncomp"          "watmin"        
#> [13] "elec"           "floor"          "walls"          "roof"          
#> [17] "asset_wardrobe" "asset_table"    "asset_chair"    "asset_khat"    
#> [21] "asset_chouki"   "asset_tv"       "asset_refrig"   "asset_bike"    
#> [25] "asset_moto"     "asset_sewmach"  "asset_mobile"

Next, we fit a linear model on the full data, with the goal of predicting the weight-for-height Z-score whz using all of the available covariate data. Let’s try it out:

lm_mod <- lm(whz ~ ., data = washb_data)
summary(lm_mod)
#> 
#> Call:
#> lm(formula = whz ~ ., data = washb_data)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -2.8890 -0.6799 -0.0169  0.6595  3.1005 
#> 
#> Coefficients:
#>                                 Estimate Std. Error t value Pr(>|t|)   
#> (Intercept)                     -1.89006    1.72022   -1.10   0.2725   
#> trHandwashing                   -0.25276    0.17032   -1.48   0.1385   
#> trNutrition                     -0.09695    0.15696   -0.62   0.5371   
#> trNutrition + WSH               -0.09587    0.16528   -0.58   0.5622   
#> trSanitation                    -0.27702    0.15846   -1.75   0.0811 . 
#> trWSH                           -0.02846    0.15967   -0.18   0.8586   
#> trWater                         -0.07148    0.15813   -0.45   0.6515   
#> fracodeN05160                    0.62355    0.30719    2.03   0.0430 * 
#> fracodeN05265                    0.38762    0.31011    1.25   0.2120   
#> fracodeN05359                    0.10187    0.31329    0.33   0.7452   
#> fracodeN06229                    0.30933    0.29766    1.04   0.2993   
#> fracodeN06453                    0.08066    0.30006    0.27   0.7882   
#> fracodeN06458                    0.43707    0.29970    1.46   0.1454   
#> fracodeN06473                    0.45406    0.30912    1.47   0.1426   
#> fracodeN06479                    0.60994    0.31463    1.94   0.0532 . 
#> fracodeN06489                    0.25923    0.31901    0.81   0.4169   
#> fracodeN06500                    0.07539    0.35794    0.21   0.8333   
#> fracodeN06502                    0.36748    0.30504    1.20   0.2290   
#> fracodeN06505                    0.20038    0.31560    0.63   0.5258   
#> fracodeN06516                    0.55455    0.29807    1.86   0.0635 . 
#> fracodeN06524                    0.49429    0.31423    1.57   0.1164   
#> fracodeN06528                    0.75966    0.31060    2.45   0.0148 * 
#> fracodeN06531                    0.36856    0.30155    1.22   0.2223   
#> fracodeN06862                    0.56932    0.29293    1.94   0.0526 . 
#> fracodeN08002                    0.36779    0.26846    1.37   0.1714   
#> month                            0.17161    0.10865    1.58   0.1149   
#> aged                            -0.00336    0.00112   -3.00   0.0029 **
#> sexmale                          0.12352    0.09203    1.34   0.1802   
#> momage                          -0.01379    0.00973   -1.42   0.1570   
#> momeduPrimary (1-5y)            -0.13214    0.15225   -0.87   0.3859   
#> momeduSecondary (>5y)            0.12632    0.16041    0.79   0.4314   
#> momheight                        0.00512    0.00919    0.56   0.5776   
#> hfiacatMildly Food Insecure      0.05804    0.19341    0.30   0.7643   
#> hfiacatModerately Food Insecure -0.01362    0.12887   -0.11   0.9159   
#> hfiacatSeverely Food Insecure   -0.13447    0.25418   -0.53   0.5970   
#> Nlt18                           -0.02557    0.04060   -0.63   0.5291   
#> Ncomp                            0.00179    0.00762    0.23   0.8145   
#> watmin                           0.01347    0.00861    1.57   0.1182   
#> elec                             0.08906    0.10700    0.83   0.4057   
#> floor                           -0.17763    0.17734   -1.00   0.3171   
#> walls                           -0.03001    0.21445   -0.14   0.8888   
#> roof                            -0.03716    0.49214   -0.08   0.9399   
#> asset_wardrobe                  -0.05754    0.13736   -0.42   0.6755   
#> asset_table                     -0.22079    0.12276   -1.80   0.0728 . 
#> asset_chair                      0.28012    0.13750    2.04   0.0422 * 
#> asset_khat                       0.02306    0.11766    0.20   0.8447   
#> asset_chouki                    -0.13943    0.14084   -0.99   0.3227   
#> asset_tv                         0.17723    0.12972    1.37   0.1726   
#> asset_refrig                     0.12613    0.23162    0.54   0.5863   
#> asset_bike                      -0.02568    0.10083   -0.25   0.7990   
#> asset_moto                      -0.32094    0.19944   -1.61   0.1083   
#> asset_sewmach                    0.05090    0.17795    0.29   0.7750   
#> asset_mobile                     0.01420    0.14972    0.09   0.9245   
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.984 on 447 degrees of freedom
#> Multiple R-squared:  0.129,  Adjusted R-squared:  0.0277 
#> F-statistic: 1.27 on 52 and 447 DF,  p-value: 0.104

We can assess how well the model fits the data by comparing the predictions of the linear model to the true outcomes observed in the data set. This is the well known (and standard) mean squared error. We can extract that from the lm model object as follows:

(err <- mean(resid(lm_mod)^2))
#> [1] 0.86568

The mean squared error is 0.86568. There is an important problem that arises when we assess the model in this way - that is, we have trained our linear regression model on the full data set and assessed the error on the full data set, using up all of our data. We, of course, are generally not interested in how well the model explains variation in the observed data; rather, we are interested in how the explanation provided by the model generalizes to a target population from which the sample is presumably derived. Having used all of our available data, we cannot honestly evaluate how well the model fits (and thus explains) variation at the population level.

To resolve this issue, cross-validation allows for a particular procedure (e.g., linear regression) to be implemented over subsets of the data, evaluating how well the procedure fits on a testing (“validation”) set, thereby providing an honest evaluation of the error.

We can easily add cross-validation to our linear regression procedure using origami. First, let us define a new function to perform linear regression on a specific partition of the data (called a “fold”):

cv_lm <- function(fold, data, reg_form) {
  # get name and index of outcome variable from regression formula
  out_var <- as.character(unlist(str_split(reg_form, " "))[1])
  out_var_ind <- as.numeric(which(colnames(data) == out_var))

  # split up data into training and validation sets
  train_data <- training(data)
  valid_data <- validation(data)

  # fit linear model on training set and predict on validation set
  mod <- lm(as.formula(reg_form), data = train_data)
  preds <- predict(mod, newdata = valid_data)
  valid_data <- as.data.frame(valid_data)

  # capture results to be returned as output
  out <- list(
    coef = data.frame(t(coef(mod))),
    SE = (preds - valid_data[, out_var_ind])^2
  )
  return(out)
}

Our cv_lm function is rather simple: we merely split the available data into a training and validation sets (using the eponymous functions provided in origami) fit the linear model on the training set, and evaluate the model on the validation set. This is a simple example of what origami considers to be cv_fun — functions for using cross-validation to perform a particular routine over an input data set. Having defined such a function, we can simply generate a set of partitions using origami’s make_folds function, and apply our cv_lm function over the resultant folds object. Below, we replicate the re-substitution estimate of the error — we did this “by hand” above — using the functions make_folds and cv_lm.

# re-substitution estimate
resub <- make_folds(washb_data, fold_fun = folds_resubstitution)[[1]]
resub_results <- cv_lm(fold = resub, data = washb_data, reg_form = "whz ~ .")
mean(resub_results$SE, na.rm = TRUE)
#> [1] 0.86568

This (nearly) matches the estimate of the error that we obtained above.

We can more honestly evaluate the error by V-fold cross-validation, which partitions the data into \(v\) subsets, fitting the model on \(v - 1\) of the subsets and evaluating on the subset that was held out for testing. This is repeated such that each subset is used for validation. We can easily apply our cv_lm function using origami’s cross_validate (n.b., by default this performs 10-fold cross-validation):

# cross-validated estimate
folds <- make_folds(washb_data)
cvlm_results <- cross_validate(
  cv_fun = cv_lm, folds = folds, data = washb_data, reg_form = "whz ~ .",
  use_future = FALSE
)
mean(cvlm_results$SE, na.rm = TRUE)
#> [1] 1.35

Having performed 10-fold cross-validation, we quickly notice that our previous estimate of the model error (by resubstitution) was a bit optimistic. The honest estimate of the error is larger!

4.7.2 Cross-validation with ARIMA

Cross-validation can also be used for forecast model selection in a time series setting. Here, the partitioning scheme mirrors the application of the forecasting model: we’ll train the data on past observations (either all available or a recent subset), and then use the ARIMA (AutoRegressive Integrated Moving Average) model fit to predict the next few observations. We consider the AirPassengers dataset again, a monthly time series of passenger air traffic in thousands of people.

data(AirPassengers)
print(AirPassengers)
#>      Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
#> 1949 112 118 132 129 121 135 148 148 136 119 104 118
#> 1950 115 126 141 135 125 149 170 170 158 133 114 140
#> 1951 145 150 178 163 172 178 199 199 184 162 146 166
#> 1952 171 180 193 181 183 218 230 242 209 191 172 194
#> 1953 196 196 236 235 229 243 264 272 237 211 180 201
#> 1954 204 188 235 227 234 264 302 293 259 229 203 229
#> 1955 242 233 267 269 270 315 364 347 312 274 237 278
#> 1956 284 277 317 313 318 374 413 405 355 306 271 306
#> 1957 315 301 356 348 355 422 465 467 404 347 305 336
#> 1958 340 318 362 348 363 435 491 505 404 359 310 337
#> 1959 360 342 406 396 420 472 548 559 463 407 362 405
#> 1960 417 391 419 461 472 535 622 606 508 461 390 432

Suppose we want to pick between two forecasting models with different arima configurations. We can do that by evaluating their forecasting performance. First, we set up the appropriate cross-validation scheme for time-series.

folds <- make_folds(AirPassengers,
  fold_fun = folds_rolling_origin,
  first_window = 36, validation_size = 24, batch = 10
)

# How many folds where generated?
length(folds)
#> [1] 9

# Examine the first 2 folds.
folds[[1]]
#> $v
#> [1] 1
#> 
#> $training_set
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> [26] 26 27 28 29 30 31 32 33 34 35 36
#> 
#> $validation_set
#>  [1] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
#> 
#> attr(,"class")
#> [1] "fold"
folds[[2]]
#> $v
#> [1] 2
#> 
#> $training_set
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46
#> 
#> $validation_set
#>  [1] 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70
#> 
#> attr(,"class")
#> [1] "fold"

By default, folds_rolling_origin will increase the size of the training set by one time point each fold. Had we followed the default option, we would have 85 folds to train! Luckily, we can pass the batch as option to folds_rolling_origin that tells it to increase the size of the training set by 10 points each iteration. Since we want to forecast the immediate next point, gap argument remains the default (0).

# make sure to load the package!
library(forecast)

# function to calculate cross-validated squared error
cv_forecasts <- function(fold, data) {
  # Get training and validation data
  train_data <- training(data)
  valid_data <- validation(data)
  valid_size <- length(valid_data)

  train_ts <- ts(log10(train_data), frequency = 12)

  # First arima model
  arima_fit <- arima(train_ts, c(0, 1, 1),
    seasonal = list(
      order = c(0, 1, 1),
      period = 12
    )
  )
  raw_arima_pred <- predict(arima_fit, n.ahead = valid_size)
  arima_pred <- 10^raw_arima_pred$pred
  arima_MSE <- mean((arima_pred - valid_data)^2)

  # Second arima model
  arima_fit2 <- arima(train_ts, c(5, 1, 1),
    seasonal = list(
      order = c(0, 1, 1),
      period = 12
    )
  )
  raw_arima_pred2 <- predict(arima_fit2, n.ahead = valid_size)
  arima_pred2 <- 10^raw_arima_pred2$pred
  arima_MSE2 <- mean((arima_pred2 - valid_data)^2)

  out <- list(mse = data.frame(
    fold = fold_index(),
    arima = arima_MSE, arima2 = arima_MSE2
  ))
  return(out)
}

mses <- cross_validate(
  cv_fun = cv_forecasts, folds = folds, data = AirPassengers,
  use_future = FALSE
)
mses$mse
#>   fold   arima  arima2
#> 1    1   68.21  137.28
#> 2    2  319.68  313.15
#> 3    3  578.35  713.36
#> 4    4  428.69  505.31
#> 5    5  407.33  371.27
#> 6    6  281.82  250.99
#> 7    7  827.56  910.12
#> 8    8 2099.59 2213.15
#> 9    9  398.37  293.38
colMeans(mses$mse[, c("arima", "arima2")])
#>  arima arima2 
#> 601.07 634.22

The arima model with no AR component seems to be a better fit for this data.

4.8 Exercises

4.8.1 Real World Data and `origami`

In this section, we review all the concepts learned via a real world data application.

We will be using the WASH Benefits data, corresponding to the effect of water quality, sanitation, hand washing, and nutritional interventions on child development in rural Bangladesh trial. The main aim of the WASH Benefits cluster-randomized controlled trial was to assess the impact of six intervention groups. In this problem set, we aim to estimate the conditional mean of the weight-for-height Z-score given treatment and all baseline covarites; we goal is also to report the performance of the Random Forest algorithm fit (Breiman 2001). We review the list of used covariates below:

outcome 
#> [1] "whz"
covars 
#>  [1] "tr"             "fracode"        "month"          "aged"          
#>  [5] "sex"            "momage"         "momedu"         "momheight"     
#>  [9] "hfiacat"        "Nlt18"          "Ncomp"          "watmin"        
#> [13] "elec"           "floor"          "walls"          "roof"          
#> [17] "asset_wardrobe" "asset_table"    "asset_chair"    "asset_khat"    
#> [21] "asset_chouki"   "asset_tv"       "asset_refrig"   "asset_bike"    
#> [25] "asset_moto"     "asset_sewmach"  "asset_mobile"

Questions:

Using Breiman’s randomForest package, predict the weight-for-height Z-score (whz) based on a subset of data (n=500) using all of the available covariates. Which loss function is appropriate for this statistical problem? Report the error of the model using all the available data to fit and evaluate the model.
Write a function to obtain the random forest fit on a specific partition of the data that aligns with cv_fun argument to cross_validate in the origami package. The function should return the appropriate loss per fold.
Using the make_folds function in origami package, define:

V-fold CV scheme with V = 5,
Monte-carlo CV scheme with V = 5 and pvalidation = 0.2,
Re-substitution scheme.

Report the risk (mean loss) and variance of the loss per fold for each of the CV schemes set in the previous question. How does the estimated risk corresponding to each CV scheme compare to the risk in Question 1?

4.8.2 Review of key concepts

Compare and contrast V-fold cross-validation with resubstitution cross-validation. What are some of the differences between the two methods? How are they similar? Describe a scenario when you would use one over the other.
What are the advantages and disadvantages of \(v\)-fold CV relative to:
1. holdout CV?
2. leave-one-out CV?
Why can’t we use V-fold cross-validation for time-series data?
Would you use rolling window or origin for non-stationary time-series? Why?

4.8.3 Ideas in action

Let \(Y\) be a binary variable with \(P(Y=1 \mid W) = 0.01\). What kind of cross-validation scheme should be used for a rare outcome? How can we do this with the origami package?

4.8.4 Advanced topics

Consider a classification problem with a large number of predictors. A statistician proposes the following analysis:
1. First screen the predictors, leaving only covariates with a strong correlation with the class labels.
2. Fit some algorithm using only the subset of highly correlated covariates.
3. Use cross-validation to estimate the tuning parameters and the performance of the proposed algorithm.
Is this a correct application of cross-validation? Why?

3 The WASH Benefits Example Dataset

5 Super (Machine) Learning