9 Stochastic Treatment Regimes

Nima Hejazi

Featuring the tmle3shift R package.

Learning Objectives

1. Differentiate stochastic treatment regimes from static, dynamic, and optimal dynamic treatment regimes.
2. Describe how a real-world data analysis may incorporate assessing the causal effects of stochastic treatment regimes.
3. Contrast a population-level (general) stochastic treatment regime from an (individualized) modified treatment policy.
4. Estimate the population-level causal effects of modified treatment policies with the tmle3shift R package.
5. Specify and interpret a set of causal effects based upon differing modified treatment policies arising from a grid of counterfactual shifts.
6. Construct marginal structural models to measure variable importance in terms of stochastic interventions, using a grid of counterfactual shifts.
7. Implement, with the tmle3shift R package, modified treatment policies that shift individual units only to the extent supported by the observed data.

9.1 Why Stochastic Interventions?

Stochastic treatment regimes, or stochastic interventions, constitute a relatively simple yet extremely flexible and expressive framework for defining realistic causal effects. In contrast to intervention regimens discussed previously, stochastic interventions may be applied to nearly any manner of treatment variable – binary, ordinal, continuous – allowing for a rich set of causal effects to be defined through this formalism. This chapter focuses on examining a few types of stochastic interventions that may be applied to continuous treatment variables, to which static and dynamic treatment regimes cannot easily be applied. Notably, the resultant causal effects conveniently are endowed with an interpretation echoing that of ordinary regression adjustment.

In the next chapter, we will introduce two alternative uses of stochastic interventions – a recently formulated intervention applicable to binary treatment variables (Kennedy, 2019) and the definition of causal effects in the presence of post-treatment, or mediating, variables. Here, we will focus on the tools provided in the tmle3shift R package, which exposes targeted minimum loss-based estimators of the causal effects of stochastic interventions that additively shift the observed value of the treatment variable. More comprehensive, technical presentations of some aspects of the material in this chapter appear in Dı́az and van der Laan (2012), Dı́az and van der Laan (2018), Hejazi, van der Laan, et al. (2020), and Hejazi (2021).

9.2 Data Structure and Notation

Let us return to the familiar data unit \(O = (W, A, Y)\), where \(W\) denote baseline covariates (e.g., age, biological sex, education level), \(A\) a treatment variable (e.g., dose of nutritional supplements), and \(Y\) an outcome of interest (e.g., disease status). Here, we consider \(A\) that are continuous-valued (i.e., \(A \in \R\)) or ordinal with many levels. For a given study, we consider observing \(n\) independent and identically distributed units \(O_1, \ldots, O_n\).

Following the roadmap, let \(O \sim P_0 \in \M\), where \(\M\) is the nonparametric statistical model, minimizing any restrictions on the form of the data-generating distribution \(P_0\). To formalize the definition of stochastic interventions and their corresponding causal effects, we introduce a structural causal model (SCM), based on Pearl (2009), to define how the system changes under posited interventions: \[\begin{align} W &= f_W(U_W) \\ \nonumber A &= f_A(W, U_A) \\ \nonumber Y &= f_Y(A, W, U_Y). \tag{9.1} \end{align}\] The set of structural equations provide a mechanistic model describing the relationships between variables composing the observed data unit \(O\). The SCM describes a temporal ordering between the variables (i.e., that \(Y\) occurs after \(A\), which occurs after \(W\)); specifies deterministic functions \(\{f_W, f_A, f_Y\}\) generating each variable \(\{W, A, Y\}\) based on those preceding it and exogenous (unobserved) variable \(\{U_W, U_A, U_Y\}\); and requires that each exogenous variable is assumed to contain all unobserved causes of the corresponding observed variable.

We can factorize the likelihood of the data unit \(O\) as follows, revealing orthogonal components of the density, \(p_0\), when evaluated on a typical observation \(o\): \[\begin{align} p_0(o) = &q_{0,Y}(y \mid A = a, W = w) \\ \nonumber &g_{0,A}(a \mid W = w) \\ \nonumber &q_{0,W}(w),\\ \nonumber \tag{9.2} \end{align}\] where \(q_{0, Y}\) is the conditional density of \(Y\) given \(\{A, W\}\) with respect to some dominating measure, \(g_{0, A}\) is the conditional density of \(A\) given \(W\) with respect to dominating measure \(\mu\), and \(q_{0, W}\) is the density of \(W\) with respect to dominating measure \(\nu\). In the interest of continuing to use familiar notation, we let \(\overline{Q}(A, W) = \E[Y \mid A, W]\), \(g(A \mid W) = g_{A}(A \mid W)\), and \(q_W\) the marginal distribution of \(W\). Importantly, the SCM parameterizes \(p_0\) in terms of the distribution of random variables \((O, U)\) modeled by the system of equations. In turn, this implies a model for the distribution of counterfactual random variables generated by interventions on the data-generating process.

9.3 Defining the Causal Effect of a Stochastic Intervention

Causal effects are defined in terms of contrasts of hypothetical interventions on the SCM (9.1). Stochastic interventions modifying components of the SCM may be thought of in two equivalent ways. A general stochastic intervention replaces the equation \(f_A\), which gives rise to \(A\), and \(g(A \mid W)\), the natural conditional density of A, with a candidate density \(g_{A_{\delta}}(A \mid W)\). In the absence of the intervention, we would consider any given value \(a \in \mathcal{A}\), the support of \(A\) – that is, the result of evaluating the function \(f_A\) at a given value \(W = w\) – as the result of a random draw from the distribution defined by the conditional density \(g(A \mid W)\), that is, \(A_{\delta} \sim g_{A_{\delta}}(\cdot \mid W)\). In applying the intervention, we simply remove the structural equation \(f_A\), instead drawing the post-intervention value \(A_{\delta}\) from the distribution defined by the candidate density \(g_{A_{\delta}}(A \mid W)\). The post-intervention value \(A_{\delta}\) is stochastically modified in the sense that it has been drawn from an arbitrary (in practice, user-defined) distribution. Note that the familiar case of static interventions can be recovered by choosing degenerate candidate distributions, which place all mass on just a single value. Stock (1989) first considered estimating the total effects of such stochastic interventions.

While there are few restrictions on the choice of the candidate post-treatment density \(g_{A_{\delta}}(A \mid W)\), in practice, it is often chosen based on knowledge of the natural (or pre-intervention) density \(g(A \mid W)\). When \(g_{A_{\delta}}(A \mid W)\) is piecewise smooth invertible (more below) (Haneuse and Rotnitzky, 2013), there is a direct correspondence between the post-intervention density \(g_{A_{\delta}}(A \mid W)\) and a function \(d(A, W; \delta)\) that maps an observed pair \(\{A, W\}\) to the post-intervention quantity \(A_{\delta}\). In such cases, the stochastic intervention, defined by \(d(A, W; \delta)\), is said to depend on the natural value of treatment and has been termed a modified treatment policy (MTP) (Dı́az and van der Laan, 2018; Haneuse and Rotnitzky, 2013; Hejazi, 2021). Haneuse and Rotnitzky (2013) and Young et al. (2014) provide detailed discussions contrasting the interpretations of the causal effects under modified treatment policies and general stochastic interventions.

Definition 9.1 (Piecewise Smooth Invertibility) For each \(w \in \mathcal{W}\), assume that the interval \(\mathcal{I}(w) = (l(w,), u(w))\) may be partitioned into subintervals \(\mathcal{I}_{\delta,j}(w): j = 1, \ldots, J(w)\) such that \(d(a, w; \delta)\) is equal to some \(d_j(a, w; \delta)\) in \(\mathcal{I}_{\delta,j}(w)\) and \(d_j(\cdot,w; \delta)\) has inverse function \(b_j(\cdot, w; \delta)\) with derivative \(b_j'(\cdot, w; \delta)\).

A stochastic intervention gives rise to a counterfactual random variable \(Y_{A_{\delta}} := f_Y(A_{\delta}, W, U_Y)\), where the counterfactual outcome \(Y_{A_{\delta}} \sim \mathcal{P}_0^{A_{\delta}}\) arises from replacing the natural value of \(A\) with \(A_{\delta}\) (whether as a draw from \(g_{A_{\delta}}(A \mid W)\) or by evaluating \(d(A, W; \delta)\)). For the remainder of this chapter, we will focus on additive MTPs of the form \[\begin{equation} d(a, w; \delta) = \begin{cases} a + \delta & \text{if } a + \delta \leq u(w) \\ a & \text{if } a + \delta > u(w), \end{cases} \tag{9.3} \end{equation}\] where \(\delta \in \mathbb{R}\) defines the degree to which an observed \(A = a\) ought to be shifted, in the context of the stratum \(W = w\), and \(l(w)\) and \(u(w)\) are the minimum and maximum values of the treatment \(A\) in the stratum \(W = w\). Consider, for example, the case where \(A\) denotes a (continuous-valued) dosage of nutritional supplements (e.g., number of vitamin pills) and assume that the distribution of \(A\) conditional on \(W = w\) has support in the interval \((l(w), u(w))\). That is, the minimum number of pills taken for an individual with in the covariate stratum defined by \(W = w\) is \(l(w)\); similarly, the maximum is \(u(w)\). Such a stochastic intervention may be interpreted as the result of a clinic policy encouraging individuals to consume \(\delta\) more vitamin pills (\(A \delta\)) than they would normally be recommended (\(A\)) based on their baseline characteristics \(W\). This class of stochastic interventions was introduced by Dı́az and van der Laan (2012) and has been further discussed in Haneuse and Rotnitzky (2013), Dı́az and van der Laan (2018), Hejazi, van der Laan, et al. (2020), and Hejazi (2021). This class of interventions may be expressed as a general stochastic intervention, as per Dı́az and van der Laan (2012), by considering the random draw \(\P_{A_{\delta}}(g_{0, A})(A = a \mid W) = g_{0,A}(a - \delta(W) \mid W)\).

In order to evaluate the causal effect of our intervention, we consider as a parameter of interest the counterfactual mean of the outcome under our stochastically modified intervention distribution. This target causal estimand is \(\psi_{0, \delta} \coloneqq \E_{P_0^{A_{\delta}}}\{Y_{A_{\delta}}\}\), the mean of the counterfactual outcome variable \(Y_{A_{\delta}}\). Dı́az and van der Laan (2018) showed that \(\psi_{0, \delta}\) may be identified by a functional of the distribution of \(O\): \[\begin{align} \psi_{0,\delta} = \int_{\mathcal{W}} \int_{\mathcal{A}} & \E_{P_0} \{Y \mid A = d(a, w), W = w\} \nonumber \\ &q_{0, A}(a \mid W = w) q_{0, W}(w) d\mu(a)d\nu(w). \tag{9.4} \end{align}\] Under certain identification conditions, which we will enumerate shortly, the statistical parameter in Equation (9.4) matches exactly the counterfactual mean \(\psi_{0, \delta}\). While this book is not concerned with the identification of causal parameters – that is, establishing statistical functionals of the observed data that have causal interpretations under certain assumptions – we review key assumptions for identifying the counterfactual mean \(\psi_{0, \delta}\) below. As the SCM introduced prior generates independent and identically distributed units \(O\), the common identification assumptions of consistency (\(Y^{A_{\delta,i}}_i = Y_i\) in the event \(A_i = d(a_i, w_i)\), for \(i = 1, \ldots, n\)) and lack of interference (\(Y^{A_{\delta,i}}_i\) does not depend on \(d(a_j, w_j)\) for \(i = 1, \ldots, n\) and \(j \neq i\)) hold. Beyond these, we require no unmeasured confounding (the analog to the randomization assumption in observational studies) and positivity.

Definition 9.2 (No Unmeasured Confounding) \(A_i \indep Y^{A_{\delta,i}}_i \mid W_i\), for \(i = 1, \ldots, n\). This is the observational study analog to the well-known randomization assumption.

Definition 9.3 (Treatment Positivity) \(a_i \in \mathcal{A} \implies d(a_i, w_i) \in \mathcal{A}\) for all \(w \in \mathcal{W}\), where \(\mathcal{A}\) denotes the support of \(A \mid W = w_i \quad \forall i = 1, \ldots n\).

9.4 Estimating the Causal Effect of a Stochastic Intervention

Dı́az and van der Laan (2012) provided a derivation of the efficient influence function (EIF), a key quantity for constructing efficient estimators, in the nonparametric model \(\M\) and developed both classical and efficient estimators of this quantity, including substitution, inverse probability weighted, one-step and targeted maximum likelihood (TML) estimators. Both the one-step and TML estimators allow for semiparametric-efficient estimation and inference on the target quantity of interest \(\psi_{0, \delta}\). As described by Dı́az and van der Laan (2018), the EIF of \(\psi_{0, \delta}\), with respect to the nonparametric model \(\M\), is \[\begin{equation} D(P_0)(x) = H(a, w)({y - \overline{Q}(a, w)}) + \overline{Q}(d(a, w), w) - \Psi(P_0), \tag{9.5} \end{equation}\] where the auxiliary covariate \(H(a,w)\) may be expressed \[\begin{equation} H(a,w) = \mathbb{I}(a + \delta < u(w)) \frac{g_0(a - \delta \mid w)} {g_0(a \mid w)} + \mathbb{I}(a + \delta \geq u(w)), \tag{9.6} \end{equation}\] which may be reduced to \[\begin{equation} H(a,w) = \frac{g_0(a - \delta \mid w)}{g_0(a \mid w)} + 1 \tag{9.7} \end{equation}\] when the treatment \(A\) lies within the limits defined by the covariate strata \(W\), that is, for \(A_i \in (u(w) - \delta, u(w))\). The efficient influence function is a key ingredient in the construction of semiparametric-efficient estimators. Next, we focus on a targeted maximum likelihood (TML) estimator, for which Dı́az and van der Laan (2018) give the following recipe:

1. Construct initial estimators \(g_n\) of \(g_0(A, W)\) and \(\overline{Q}_n\) of \(\overline{Q}_0(A, W)\), ideally using data-adaptive regression techniques.
2. For each observation \(i\), compute an estimate \(H_n(a_i, w_i)\) of the auxiliary covariate \(H(a_i,w_i)\).
3. Construct the one-dimensional logistic regression model, \[ \text{logit}\overline{Q}_{\epsilon, n}(a, w) = \text{logit}\overline{Q}_n(a, w) + \epsilon H_n(a, w),\] or an analogous regression model incorporating \(H_n\) as weights. Estimate the regression model’s parameter \(\epsilon\), obtaining \(\epsilon_n\). The outcome of this regression model yields \(\overline{Q}_n^{\star}\).
4. Compute TML estimator \(\Psi_n\) of the target parameter, defining update \(\overline{Q}_n^{\star}\) of the initial estimate \(\overline{Q}_{n, \epsilon_n}\): \[\begin{equation} \psi_n = \Psi(P_n^{\star}) = \frac{1}{n} \sum_{i = 1}^n \overline{Q}_n^{\star}(d(A_i, W_i), W_i). \tag{9.8} \end{equation}\]

As discussed previously, TML estimators are constructed so as to be asymptotically linear and are usually doubly robust. Asymptotic linearity means that the asymptotic difference between the estimator \(\psi_n\) and the target parameter \(\psi_0\) can be expressed in terms of the EIF, that is, \[\begin{equation} \sqrt{n}(\psi_n - \psi_0) = \frac{1}{\sqrt{n}}\sum_{i=1}^n D(P_0)(O_i) + o_p(1). \tag{9.9} \end{equation}\] Together with regularity, asymptotic linearity establishes a class of estimators whose asymptotic variance is bounded from below by the asymptotic variance of the EIF. This means that such estimators are solutions to the EIF estimating equation (i.e., plugging the TML estimator \(\psi_n\) into the EIF equation results in a solution close to zero) and that their sampling variance may be approximated by the variance of the EIF in closed form. This latter fact is computationally convenient, as resampling methods (e.g., the bootstrap) are not strictly necessary for variance estimation. A central limit theorem establishes that the asymptotic distribution of the estimator \(\psi_n\) is centered at \(\psi_0\) and is Gaussian: \[\begin{equation} \sqrt{n}(\psi_n - \psi_0) \to \text{Normal}(0, \sigma^2(D(P_0))). \tag{9.10} \end{equation}\] Thus, an estimate \(\sigma_n^2\) of the variance \(\sigma^2(D(P_0))\) may be computed \[\begin{equation} \sigma_n^2 = \frac{1}{n} \sum_{i = 1}^{n} D^2(\overline{Q}_n^{\star}, g_n)(O_i), \tag{9.11} \end{equation}\] allowing for Wald-style confidence intervals at coverage level \((1 - \alpha)\) to be computed as \(\psi_n \pm z_{(1 - \alpha/2)} \cdot \sigma_n / \sqrt{n}\). Under certain conditions, the resampling based on the bootstrap may also be used to compute \(\sigma_n^2\) (van der Laan and Rose, 2011).

9.5 Interpreting the Causal Effect of a Stochastic Intervention

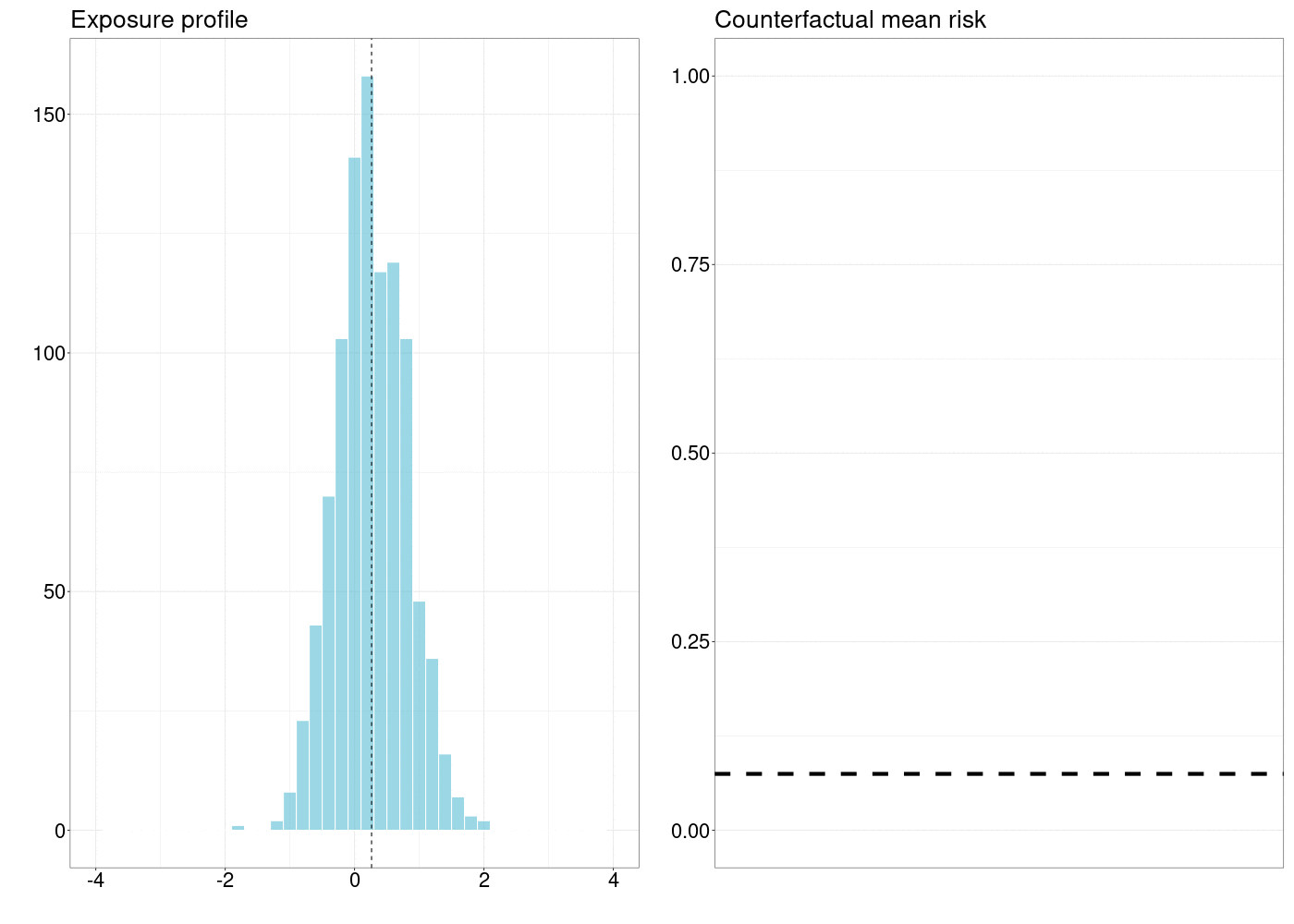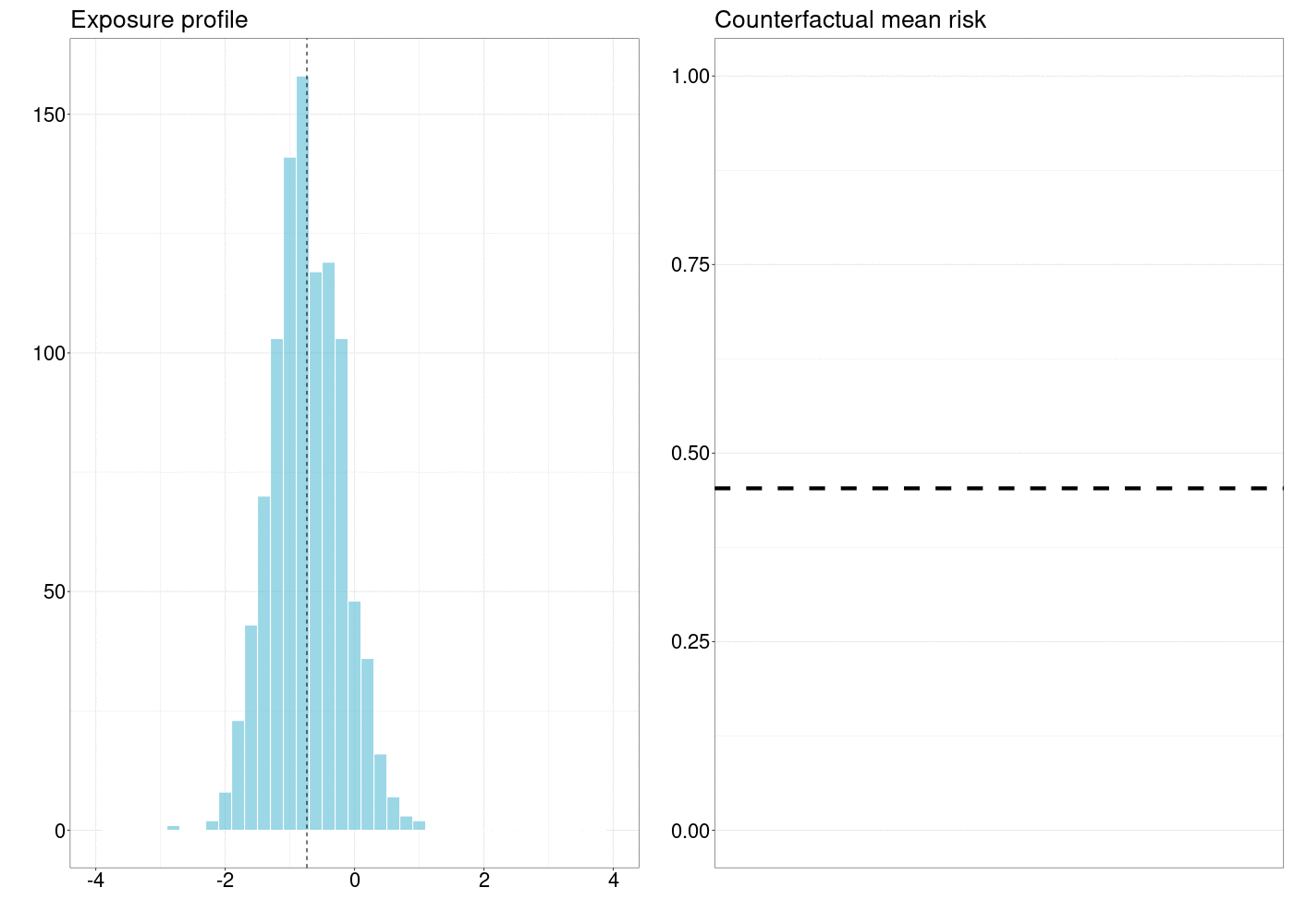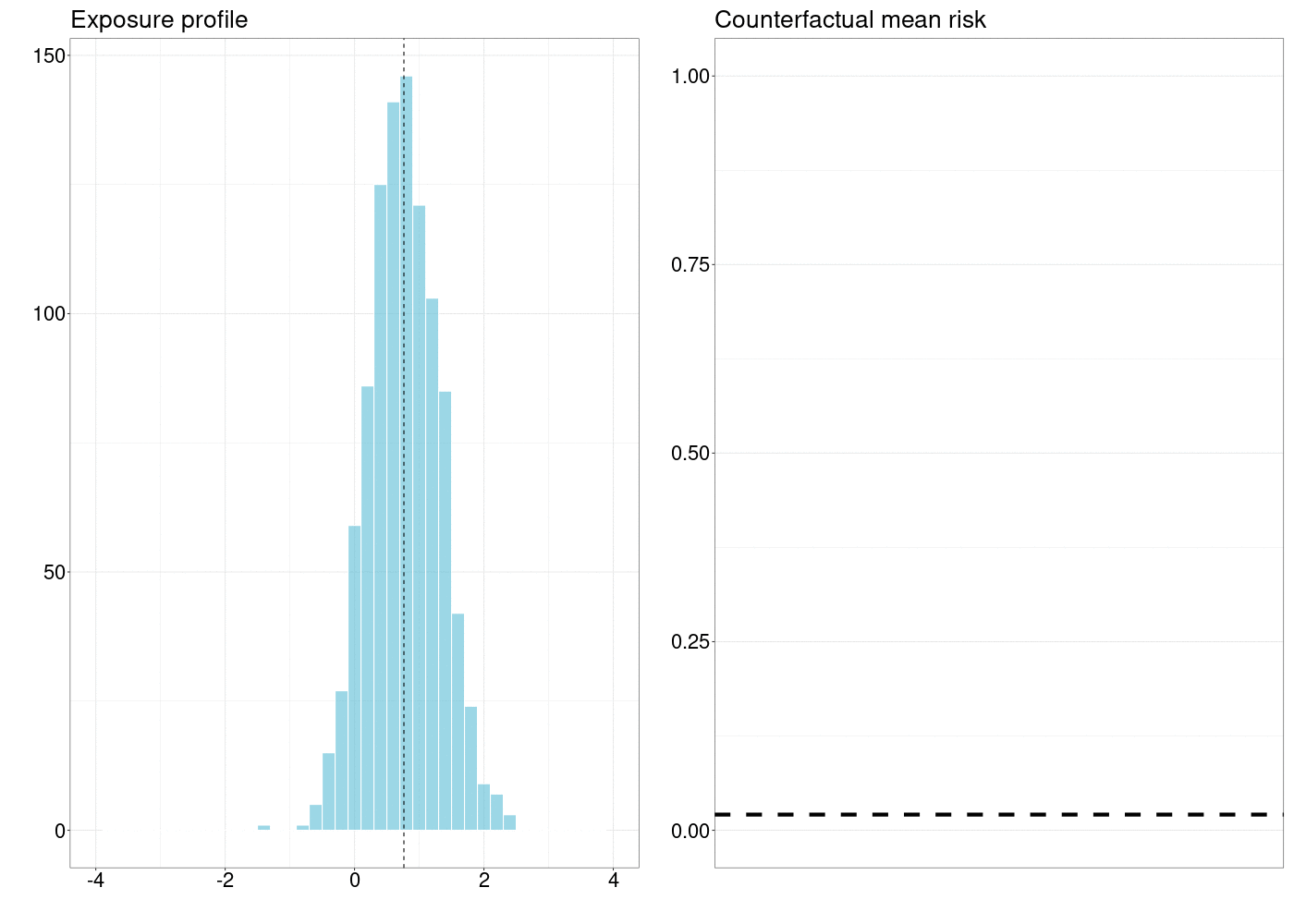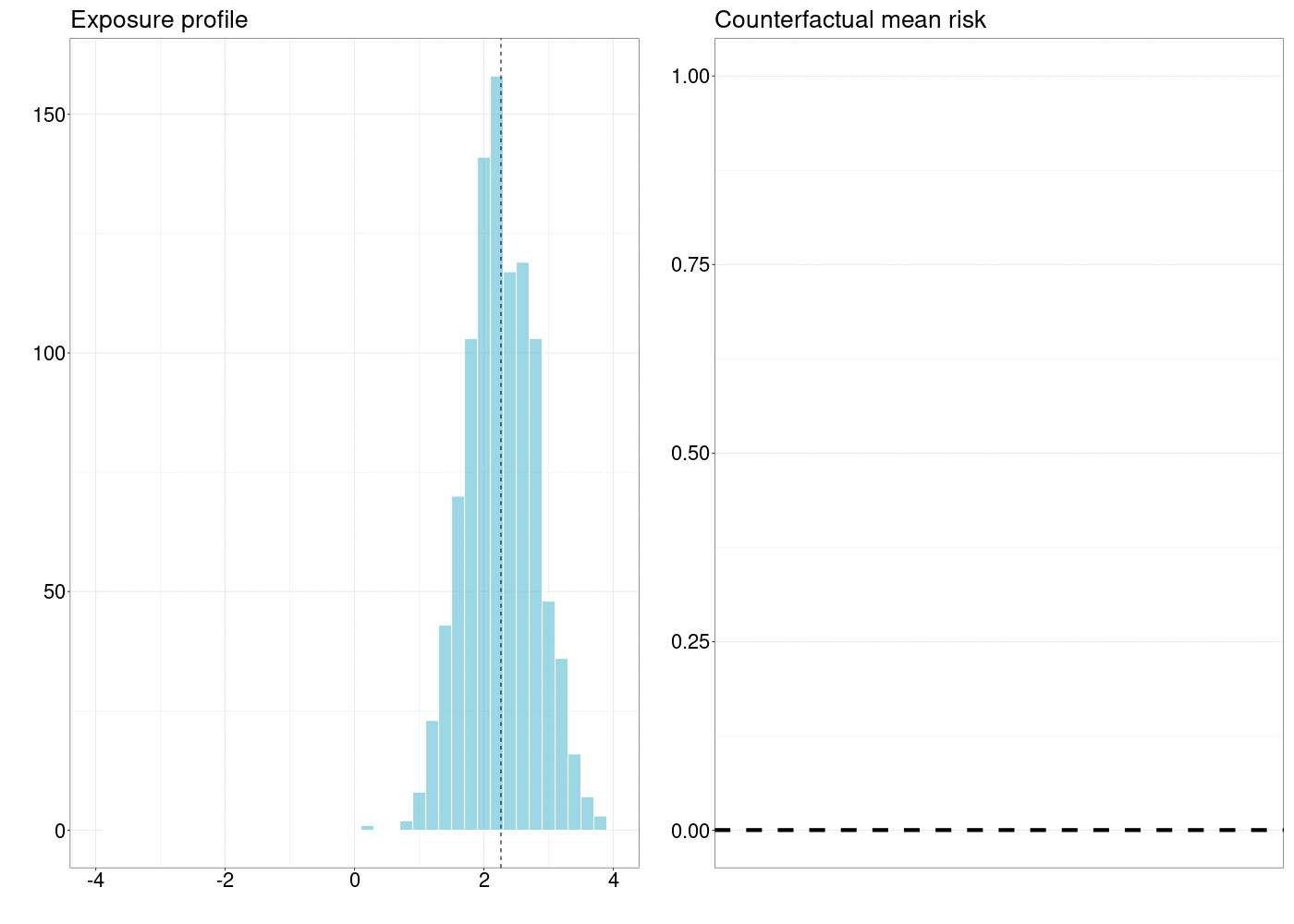
FIGURE 5.1: How a counterfactual outcome changes as the natural treatment distribution is shifted by a simple stochastic intervention

9.6 Evaluating the Causal Effect of a Stochastic Intervention

To start, let’s load the packages we’ll be using throughout our simple data example

library(data.table)
library(haldensify)
library(sl3)
library(tmle3)
library(tmle3shift)

We need to estimate two components of the likelihood in order to construct a TML estimator. The first of these components is the outcome regression, \(\overline{Q}_n\), which is a simple regression of the form \(\E[Y \mid A,W]\). An estimate for such a quantity may be constructed using the Super Learner algorithm. We construct the components of an sl3-style Super Learner for a regression below, using a small variety of parametric and nonparametric regression techniques:

# learners used for conditional mean of the outcome
mean_lrnr <- Lrnr_mean$new()
fglm_lrnr <- Lrnr_glm_fast$new()
rf_lrnr <- Lrnr_ranger$new()
hal_lrnr <- Lrnr_hal9001$new(max_degree = 3, n_folds = 3)

# SL for the outcome regression
sl_reg_lrnr <- Lrnr_sl$new(
  learners = list(mean_lrnr, fglm_lrnr, rf_lrnr, hal_lrnr),
  metalearner = Lrnr_nnls$new()
)

The second of these is an estimate of the treatment mechanism, \(g_n\), i.e., the generalized propensity score. In the case of a continuous intervention node \(A\), such a quantity takes the form \(p(A \mid W)\), which is a conditional density. Generally speaking, conditional density estimation is a challenging problem that has received much attention in the literature. To estimate the treatment mechanism, we must make use of learning algorithms specifically suited to conditional density estimation; a list of such learners may be extracted from sl3 by using sl3_list_learners():

sl3_list_learners("density")
[1] "Lrnr_density_discretize"     "Lrnr_density_hse"           
[3] "Lrnr_density_semiparametric" "Lrnr_haldensify"            
[5] "Lrnr_solnp_density"         

To proceed, we’ll select two of the above learners, Lrnr_haldensify for using the highly adaptive lasso for conditional density estimation, based on an algorithm given by Dı́az and van der Laan (2011) and implemented in Hejazi, Benkeser, et al. (2022), and semiparametric location-scale conditional density estimators implemented in the sl3 package. A Super Learner may be constructed by pooling estimates from each of these modified conditional density regression techniques (note that we exclude the approach based on the haldensify learner from our Super Learner on account of the computationally intensive nature of the approach).

# learners used for conditional densities for (g_n)
haldensify_lrnr <- Lrnr_haldensify$new(
  n_bins = c(5, 10, 20),
  lambda_seq = exp(seq(-1, -10, length = 200))
)
# semiparametric density estimator with homoscedastic errors (HOSE)
hose_hal_lrnr <- make_learner(Lrnr_density_semiparametric,
  mean_learner = hal_lrnr
)
# semiparametric density estimator with heteroscedastic errors (HESE)
hese_rf_glm_lrnr <- make_learner(Lrnr_density_semiparametric,
  mean_learner = rf_lrnr,
  var_learner = fglm_lrnr
)

# SL for the conditional treatment density
sl_dens_lrnr <- Lrnr_sl$new(
  learners = list(hose_hal_lrnr, hese_rf_glm_lrnr),
  metalearner = Lrnr_solnp_density$new()
)

Finally, we construct a learner_list object for use in constructing a TML estimator of our target parameter of interest:

learner_list <- list(Y = sl_reg_lrnr, A = sl_dens_lrnr)

The learner_list object above specifies the role that each of the ensemble learners we have generated is to play in computing initial estimators to be used in building a TMLE for the parameter of interest here. In particular, it makes explicit the fact that our Q_learner is used in fitting the outcome regression while our g_learner is used in estimating the treatment mechanism.

9.6.1 Example with Simulated Data

# simulate simple data for tmle-shift sketch
n_obs <- 400 # number of observations
tx_mult <- 2 # multiplier for the effect of W = 1 on the treatment

## baseline covariates -- simple, binary
W <- replicate(2, rbinom(n_obs, 1, 0.5))

## create treatment based on baseline W
A <- rnorm(n_obs, mean = tx_mult * W, sd = 1)

## create outcome as a linear function of A, W + white noise
Y <- rbinom(n_obs, 1, prob = plogis(A + W))

# organize data and nodes for tmle3
data <- data.table(W, A, Y)
setnames(data, c("W1", "W2", "A", "Y"))
node_list <- list(
  W = c("W1", "W2"),
  A = "A",
  Y = "Y"
)
head(data)
   W1 W2        A Y
1:  1  1  0.27165 1
2:  0  0 -0.66337 1
3:  0  0  0.11337 0
4:  0  1 -0.73256 0
5:  1  1  0.38884 1
6:  0  0  0.04399 0

The above composes our observed data structure \(O = (W, A, Y)\). To formally express this fact using the tlverse grammar introduced by the tmle3 package, we create a single data object and specify the functional relationships between the nodes in the directed acyclic graph (DAG) via an SCM, reflected in the node list we set up.

We now have an observed data structure (data) and a specification of the role that each variable in the data set plays as the nodes in a DAG.

To start, we will initialize a specification for the TMLE of our parameter of interest (called a tmle3_Spec in the tlverse nomenclature) simply by calling tmle_shift. We specify the argument shift_val = 0.5 when initializing the tmle3_Spec object to communicate that we’re interested in a shift of \(0.5\) on the scale of the treatment \(A\) – that is, we specify \(\delta = 0.5\) (an arbitrarily chosen value for this example).

# initialize a tmle specification
tmle_spec <- tmle_shift(
  shift_val = 0.5,
  shift_fxn = shift_additive,
  shift_fxn_inv = shift_additive_inv
)

As seen above, the tmle_shift specification object (like all tmle3_Spec objects) does not store the data for our specific analysis of interest. Later, we’ll see that passing a data object directly to the tmle3 wrapper function, alongside the instantiated tmle_spec, will serve to construct a tmle3_Task object internally (see the tmle3 documentation for details).

9.6.2 Targeted Estimation of Stochastic Interventions Effects

tmle_fit <- tmle3(tmle_spec, data, node_list, learner_list)

Iter: 1 fn: 548.8338     Pars:  0.94736 0.05264
Iter: 2 fn: 548.8338     Pars:  0.94736 0.05264
solnp--> Completed in 2 iterations
tmle_fit
A tmle3_Fit that took 1 step(s)
   type         param init_est tmle_est      se  lower  upper psi_transformed
1:  TSM E[Y_{A=NULL}]   0.7645   0.7601 0.02284 0.7154 0.8049          0.7601
   lower_transformed upper_transformed
1:            0.7154            0.8049

The print method of the resultant tmle_fit object conveniently displays the results of computing our TML estimator \(\psi_n\). The standard error estimate is computed based on the estimated EIF.

9.7 Selecting Stable Stochastic Interventions

At times, a particular choice of the shift parameter \(\delta\) may lead to positivity violations and downstream instability in the estimation process. In order to curb such issues, we can make choices of \(\delta\) based on the impact of the candidate values on the estimator. Recall that a simplified expression of the auxiliary covariate for the TMLE of \(\psi\) is \(H = \frac{g(a - \delta \mid w)}{g(a \mid w)}\), where \(g(a - \delta \mid w)\) is defined by the stochastic intervention of interest. We can design our stochastic intervention to avoid violations of the positivity assumption by by considering a bound \(C(\delta) = \frac{g(a - \delta \mid w)}{g(a \mid w)} < M\), where \(M\) is a potentially user-specified upper bound of \(C(\delta)\). Note that \(C(\delta)\) corresponds to the inverse weight assigned to the unit with counterfactual treatment value \(A = a + \delta\), natural treatment value \(A = a\), and covariates \(W = w\). So, \(C(\delta)\) can be viewed as a measure of the influence that a given observation has on the estimator \(\psi_n\). By limiting \(C(\delta)\), whether through a choice of \(M\) or \(\delta\), we can limit the potential instability of our estimator. We can formalize this procedure by defining a new shift function \(\delta(A, W)\): \[\begin{equation} \delta(a, w) = \begin{cases} \delta, & \delta_{\text{min}}(a,w) \leq \delta \leq \delta_{\text{max}}(a,w) \\ \delta_{\text{max}}(a,w), & \delta \geq \delta_{\text{max}}(a,w) \\ \delta_{\text{min}}(a,w), & \delta \leq \delta_{\text{min}}(a,w) \\ \end{cases}, \tag{9.12} \end{equation}\] where \[\delta_{\text{max}}(a, w) = \text{argmax}_{\left\{\delta \geq 0, \frac{g(a - \delta \mid w)}{g(a \mid w)} \leq M \right\}} \frac{g(a - \delta \mid w)}{g(a \mid w)}\] and \[\delta_{\text{min}}(a, w) = \text{argmin}_{\left\{\delta \leq 0, \frac{g(a - \delta \mid w)}{g(a \mid w)} \leq M \right\}} \frac{g(a - \delta \mid w)}{g(a \mid w)}.\]

The above provides a strategy for implementing a shift at the level of a given observation \((a_i, w_i)\), thereby allowing for all observations to be shifted to an appropriate value, whether \(\delta_{\text{min}}\), \(\delta\), or \(\delta_{\text{max}}\). The tmle3shift package implements the functions shift_additive_bounded and shift_additive_bounded_inv, which define a variation of this strategy: \[\begin{equation} \delta(a, w) = \begin{cases} \delta, & C(\delta) \leq M \\ 0, \text{otherwise} \\ \end{cases}, \tag{9.13} \end{equation}\] corresponding to an intervention in which the natural value of treatment \(A = a\) is shifted by a value \(\delta\) when the ratio \(C(\delta)\) of the post-intervention density \(g(a - \delta \mid w)\) to the natural treatment density \(g(a \mid w)\) does not exceed a bound \(M\). When \(C(\delta)\) exceeds the bound \(M\), the stochastic intervention exempts the given unit from the treatment modification, leaving them to their natural value of treatment \(A = a\).

9.7.1 Initializing vimshift through its tmle3_Spec

To start, we will initialize a specification for the TMLE of our parameter of interest (called a tmle3_Spec in the tlverse nomenclature) simply by calling tmle_shift. We specify the argument shift_grid = seq(-1, 1, by = 1) when initializing the tmle3_Spec object to communicate that we’re interested in assessing the mean counterfactual outcome over a grid of shifts \(\delta \in \{-1, 0, 1\}\) on the scale of the treatment \(A\) (n.b., we make an arbitrary choice of shift values for this example).

# what's the grid of shifts we wish to consider?
delta_grid <- seq(-1, 1, 1)

# initialize a tmle specification
tmle_spec <- tmle_vimshift_delta(
  shift_grid = delta_grid,
  max_shifted_ratio = 2
)

As seen above, the tmle_vimshift specification object (like all tmle3_Spec objects) does not store the data for our specific analysis of interest. Later, we’ll see that passing a data object directly to the tmle3 wrapper function, alongside the instantiated tmle_spec, will serve to construct a tmle3_Task object internally (see the tmle3 documentation for details).

9.7.2 Targeted Estimation of Stochastic Interventions Effects

One may walk through the step-by-step procedure for fitting the TML estimator of the mean counterfactual outcome under each shift in the grid, using the machinery exposed by the tmle3 R package.

One may invoke the tmle3 wrapper function (a user-facing convenience utility) to fit the series of TML estimators (one for each parameter defined by the grid delta) in a single function call:

tmle_fit <- tmle3(tmle_spec, data, node_list, learner_list)

Iter: 1 fn: 547.4323     Pars:  0.9998973 0.0001027
Iter: 2 fn: 547.4323     Pars:  0.99997059 0.00002941
solnp--> Completed in 2 iterations
tmle_fit
A tmle3_Fit that took 1 step(s)
         type          param init_est tmle_est       se  lower  upper
1:        TSM  E[Y_{A=NULL}]   0.5681   0.5718 0.021416 0.5299 0.6138
2:        TSM  E[Y_{A=NULL}]   0.6975   0.6975 0.022996 0.6524 0.7426
3:        TSM  E[Y_{A=NULL}]   0.8167   0.8155 0.017110 0.7819 0.8490
4: MSM_linear MSM(intercept)   0.6941   0.6949 0.019107 0.6575 0.7324
5: MSM_linear     MSM(slope)   0.1243   0.1218 0.008603 0.1049 0.1387
   psi_transformed lower_transformed upper_transformed
1:          0.5718            0.5299            0.6138
2:          0.6975            0.6524            0.7426
3:          0.8155            0.7819            0.8490
4:          0.6949            0.6575            0.7324
5:          0.1218            0.1049            0.1387

Remark: The print method of the resultant tmle_fit object conveniently displays the results from computing our TML estimator.

9.7.3 Estimation and Inference with Marginal Structural Models

It can be challenging to select a value of the shift parameter \(\delta\) in advance. One solution is to specify a grid of such shifts \(\delta\) to be used in defining a set of related stochastic interventions (Hejazi, van der Laan, et al., 2020). When we consider estimating the counterfactual mean \(\psi_n\) under several choices of \(\delta\), a single summary measure of these estimated quantities can be established through working marginal structural models (MSMs). Summarizing the estimates \(\psi_n\) through a working MSM allows for inference on the trend appearing through the grid in \(\delta\), which may be evaluating through a simple hypothesis test on the slope parameter \(\beta_0\) of the working MSM. Consider a grid of \(\delta\), \(\{\delta_1, \ldots, \delta_k\}\), corresponding to counterfactual means \(\{\psi_{\delta_1}, \ldots, \psi_{\delta_k}\}\). Next, let \(\psi(\delta) = (\psi_{\delta}: \delta)\) denote the grid of counterfactual means in the grid defined by \(\delta\) and let \(\psi_n(\delta)\) denote TML estimators of \(\psi(\delta)\). The MSM summarizing the change in \(\psi_n\) as a function of \(\delta\) may be expressed \(m_{\beta}(\psi_{\delta}) = \beta_0 + \beta_1 \delta\). This simple working model summarizes the changes in \(\psi_{\delta}\) as a function of the parameters \((\beta_0, \beta_1)\), where the latter is the slope of the line resulting from projecting the counterfactual means onto this simple two-parameter working model.

A more general expression for the MSM \(m_{\beta}(\delta)\) is \(\beta_0 = \text{argmin}_{\beta} \sum_{\delta}(\psi_{\delta}(P_0) - m_{\beta}(\delta))^2 h(\delta)\), the solution to the estimating equation \[u(\beta, (\psi_{\delta}: \delta)) = \sum_{\delta}h(\delta) \left(\psi_{\delta}(P_0) - m_{\beta}(\delta) \right) \frac{d}{d\beta} m_{\beta}(\delta) = 0.\] Now, say, \(\psi = (\psi(\delta): \delta)\) is d-dimensional. We may express the EIF of the MSM parameter \(\beta_0\) in terms of the EIFs of the individual counterfactual means: \[\begin{align} D_{\beta}(O) = &\left(\sum_{\delta} h(\delta) \frac{d}{d\beta} m_{\beta}(\delta) \frac{d}{d\beta} m_{\beta}(\delta)^t \right)^{-1} \\ \nonumber &\sum_{\delta} h(\delta) \frac{d}{d\beta} m_{\beta}(\delta) D_{\psi_{\delta}}(O). \tag{9.14} \end{align}\] Here, in Equation (9.14), the first component is of dimension \(d \times d\) and the second is of dimension \(d \times 1\). In the above, we assume a linear working MSM; however, an analogous procedure may be applied for working MSMs based on GLMs.

Above, we utilized a straightforward application of the delta method to obtain the EIF of \(\beta\). Inference for this parameter of a working MSM follows from evaluation of its EIF \(D_{\beta}\), which is expressed in terms of the EIFs of each of the corresponding estimates \(\psi_n(\delta)\). The limit distribution of \(\beta_n\) may be expressed \[\sqrt{n}(\beta_n - \beta_0) \to N(0, \Sigma),\] where \(\Sigma\) is the empirical covariance matrix of \(D_{\beta}(O)\). With this, we can not only estimate the trend through the counterfactual means across a grid in \(\delta\), but we can also evaluate whether the slope estimate is statistically significant, in terms of hypothesis tests of the form \((H_0: \beta_0 = 0; H_1: \beta_0 \neq 0)\) and equivalent Wald-style confidence intervals. Note that the estimator \(\beta_n\) of the parameter \(\beta_0\) of the MSM is asymptotically linear (and, in fact, a TML estimator) as a consequence of its construction from individual TML estimators.

The strategy just discussed constructs an estimate \(\beta_n\) of the working MSM slope \(\beta_0\) by first evaluating the TML estimates of the counterfactual means \(\psi_{n,\delta}\) in the grid \(\{\delta_1, \ldots, \delta_k\}\); however, this is not necessarily the best strategy, especially when giving consideration to estimation stability in small samples. In smaller samples, it may be prudent to perform TML estimation targeting directly the parameter \(\beta_0\), as opposed to constructing it by applying the delta method to several independently targeted TML estimates.

To do so, consider a TML estimator targeting \(\beta_0\) (the parameter of the working MSM \(m_{\beta}\)), which uses a targeting update step of the form \(\overline{Q}_{n, \epsilon}(A,W) = \overline{Q}_n(A,W) + \epsilon (H_{\beta_0}(g), H_{\beta_1}(g))\), for all \(\delta\), where \(H_{\beta_0}(g)\) is the auxiliary covariate for \(\beta_0\) (the intercept) and \(H_{\beta}(g)\) is the auxiliary covariate for \(\beta_1\) (the slope). Note that the forms of these auxiliary covariates depend on the EIF \(D_{\beta}\). Such a TML estimator avoids estimating each of the \(\psi_{\delta}\) in the grid directly, instead cleverly concatenating their auxiliary covariates into those appropriate for \(\beta_0\) and \(\beta_1\). To construct a targeted maximum likelihood estimator that directly targets the parameters of the working MSM, we may use the tmle_vimshift_msm Spec (instead of the tmle_vimshift_delta Spec).

# initialize a tmle specification
tmle_msm_spec <- tmle_vimshift_msm(
  shift_grid = delta_grid,
  max_shifted_ratio = 2
)

# fit the TML estimator and examine the results
tmle_msm_fit <- tmle3(tmle_msm_spec, data, node_list, learner_list)
tmle_msm_fit

9.7.4 Example with the WASH Benefits Data

To complete our walk through, let’s turn to using stochastic interventions to investigate the data from the WASH Benefits trial. To start, let’s load the data, convert all columns to be of class numeric, and take a quick look at it

washb_data <- fread(
  paste0(
    "https://raw.githubusercontent.com/tlverse/tlverse-data/master/",
    "wash-benefits/washb_data.csv"
  ),
  stringsAsFactors = TRUE
)
washb_data <- washb_data[!is.na(momage), lapply(.SD, as.numeric)]
head(washb_data, 3)
     whz tr fracode month aged sex momage momedu momheight hfiacat Nlt18 Ncomp
1:  0.00  1       4     9  268   2     30      2     146.4       1     3    11
2: -1.16  1       4     9  286   2     25      2     148.8       3     2     4
3: -1.05  1      20     9  264   2     25      2     152.2       1     1    10
   watmin elec floor walls roof asset_wardrobe asset_table asset_chair
1:      0    1     0     1    1              0           1           1
2:      0    1     0     1    1              0           1           0
3:      0    0     0     1    1              0           0           1
   asset_khat asset_chouki asset_tv asset_refrig asset_bike asset_moto
1:          1            0        1            0          0          0
2:          1            1        0            0          0          0
3:          0            1        0            0          0          0
   asset_sewmach asset_mobile
1:             0            1
2:             0            1
3:             0            1

Next, we specify our NPSEM via the node_list object. For our example analysis, we’ll consider the outcome to be the weight-for-height Z-score (as in previous chapters), the intervention of interest to be the mother’s age at time of child’s birth, and take all other covariates to be potential confounders.

node_list <- list(
  W = names(washb_data)[!(names(washb_data) %in%
    c("whz", "momage"))],
  A = "momage",
  Y = "whz"
)

Were we to consider the counterfactual weight-for-height Z-score under shifts in the age of the mother at child’s birth, how would we interpret estimates of our parameter? To simplify our interpretation, consider a shift of just a year in the mother’s age (i.e., \(\delta = 1\)); in this setting, a stochastic intervention would correspond to a policy advocating that potential mothers defer having a child for a single calendar year, possibly implemented through an encouragement design deployed in a clinical setting.

For this example, we’ll use the variable importance strategy of considering a grid of stochastic interventions to evaluate the weight-for-height Z-score under a shift in the mother’s age down by two years (\(\delta = -2\)) or up by two years (\(\delta = 2\)). To do this, we simply initialize a Spec tmle_vimshift_delta just as we did in a previous example:

# initialize a tmle specification for the variable importance parameter
washb_vim_spec <- tmle_vimshift_delta(
  shift_grid = c(-2, 2),
  max_shifted_ratio = 2
)

Prior to running our analysis, we’ll modify the learner_list object we had created such that the density estimation procedure we rely on will be only the location-scale conditional density estimation procedure, as the nonparametric conditional density approach based on the highly adaptive lasso (Benkeser and van der Laan, 2016; Coyle et al., 2022; Dı́az and van der Laan, 2011; Hejazi, Coyle, et al., 2020; Hejazi, Benkeser, et al., 2022) is currently unable to accommodate larger datasets.

# we need to turn on cross-validation for the HOSE learner
cv_hose_hal_lrnr <- Lrnr_cv$new(
  learner = hose_hal_lrnr,
  full_fit = TRUE
)

# modify learner list, using existing SL for Q fit
learner_list <- list(Y = sl_reg_lrnr, A = cv_hose_hal_lrnr)

Having made the above preparations, we’re now ready to estimate the counterfactual mean of the weight-for-height Z-score under a small grid of shifts in the mother’s age at child’s birth. Just as before, we do this through a simple call to our tmle3 wrapper function:

washb_tmle_fit <- tmle3(washb_vim_spec, washb_data, node_list, learner_list)
washb_tmle_fit

---

9.8 Exercises

9.8.1 The Ideas in Action

Exercise 9.1 Set the sl3 library of algorithms for the Super Learner to a simple, interpretable library and use this new library to estimate the counterfactual mean of mother’s age at child’s birth (momage) under a shift \(\delta = 0\). What does this counterfactual mean equate to in terms of the observed data?

Solution. Forthcoming

Exercise 9.2 Using a grid of values of the shift parameter \(\delta\) (e.g., \(\{-1, 0, +1\}\)), repeat the analysis on the variable chosen in the preceding question, summarizing the trend for this sequence of shifts using a marginal structural model.

Solution. Forthcoming

Exercise 9.3 Repeat the preceding analysis, using the same grid of shifts, but instead directly targeting the parameters of the marginal structural model. Interpret the results – that is, what does the slope of the marginal structural model tell us about the trend across the chosen sequence of shifts?

Solution. Forthcoming

9.8.2 Review of Key Concepts

Exercise 9.4 Describe two (equivalent) ways in which the causal effects of stochastic interventions may be interpreted.

Solution. Forthcoming

Exercise 9.5 How can the information provided by estimates across several shifts \(\{ \delta_1, \ldots, \delta_k \}\) and the marginal structural model parameter summarizing the trend in \(\delta\) be used to enrich the interpretation of our findings?

Solution. Forthcoming

Exercise 9.6 What advantages, if any, are there to targeting directly the parameters of a marginal structural model?

Solution. Forthcoming